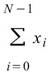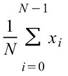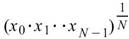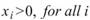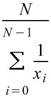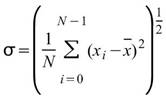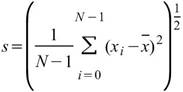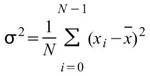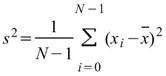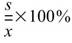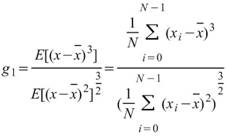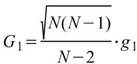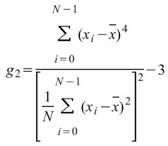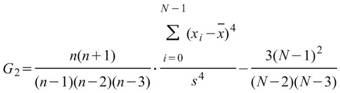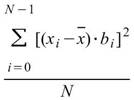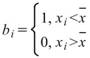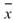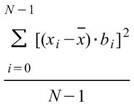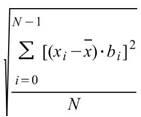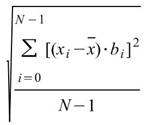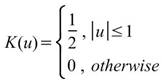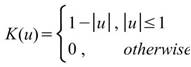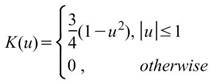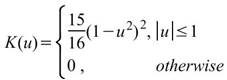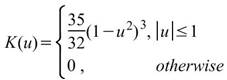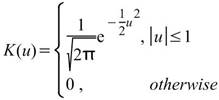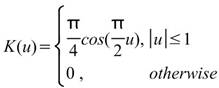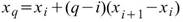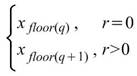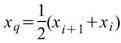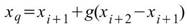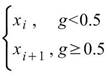本模組群提供計算訊號各項統計值之工具,包含的模組如下:
-
Basic Statistics:計算訊號之基本統計參數,諸如最大值、最小值、平均、標準差等。
-
Covariance Matrix:計算多筆訊號之共變異數矩陣。
-
Correlation Matrix:計算多筆訊號之相關係數矩陣。
-
Equiphase Statistics:計算輸入訊號之等相位統計值。
-
Kernel Smoothing Density:利用特定之核函數(kernel funciton)計算出輸入訊號之機率密度線,並可平滑之。
-
Orthogonality Matrix:對多筆訊號計算出彼此之正交性矩陣。
-
Quartiles and Quantiles:可計算訊號之各種分位數與四分位數。
-
Rolling Statistics:計算訊號之滾動統計值。
-
Hypothesis Test:對資料及訊號進行設定假設、選擇檢定方法、判斷是否接受假設。
-
Linear Regression:對訊號取出趨勢直線,對兩組資料的相關性找出最佳直線。
Basic statistics 是一項讓使用者能快速檢視輸入數列之基本統計數據的工具。
說明:
令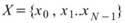 代表長度為 N 的數列(不限定為時間序列), Basic
Statistics 將計算下列各項統計資訊。
代表長度為 N 的數列(不限定為時間序列), Basic
Statistics 將計算下列各項統計資訊。
|
統計值 |
數學式 |
說明 |
|
Sum |
|
資料中每個元素的總合。 |
|
Min |
- |
資料中的最小值。 |
|
Max |
- |
資料中的最大值。 |
|
Mean |
|
計算資料算數平均值。 |
|
Geometric Mean |
|
計算資料幾何平均值,多用於計算比率、人口成長等呈幾何變化的數列。 |
|
Harmonic Mean |
|
計算調合平均數,多用於計算平均速率。 |
|
Trimmed Mean |
- |
截頭尾平均數,算法為先設定的濾除比例 ( % ),將資料X 排序後,頭尾各濾除比列的部份的數列部份濾除,剩下的訊號值作算數平均,如此可排除數列中極端值所造成的影響。 |
|
Median |
- |
資料的中位數。 |
|
StdDev |
|
標準差,可推估母體資料距離平均值的離散程度,假設此資料為樣本,無法利用樣本去推估母體標準差 ( Biased Moment Estimation)。 |
|
|
當此資料為樣本,計算樣本不偏估之標準差 ( Unbiased Moment Estimation ),可以用來推估母體標準差。 |
|
|
Variance |
|
母體資料的變異數 (標準差的平方),假設此資料為樣本,無法利用樣本去推估母體變異數( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之變異數 ( UnbiasedMoment Estimation ),可以用來推估母體變異數。 |
|
|
Coefficient of Variation |
|
母體變異係數,表示標準差佔平均值的百分比,用於比較多組資料個別間的離散程度 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之變異係數 ( Unbiased Moment Estimation ),可以用來推估母體變異係數。 |
|
|
Skewness |
|
母體偏度,用以推估資料分佈圖形的對稱性,即第三中央慣性矩除以標準偏差的三次方 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之偏度 (Unbiased Moment Estimation ),可以用來推估母體偏度。 |
|
|
Kurtosis |
|
母體峰度,用來推估資料分佈圖形是高瘦或者是矮胖,即第四中央慣性矩除以標準偏差的四次方減三 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之峰度 ( Unbiased Moment Estimation ),可以用來推估母體峰度。 |
|
|
Semivariance |
|
計算母體資料之半變異數,預設以數列平均值 |
|
|
當此資料為樣本,計算樣本不偏估之樣本半變異數( Unbiased Moment Estimation ),可以用來推估母體之半變異數。 |
|
|
Semi Standard Deviation |
|
將母體資料之半變異數 (Biased Moment Estimation ) 開根號即為資料之半標準偏差 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之樣本半標準差( Unbiased Moment Estimation ),可以用來推估母體半標準差。 |
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel)或多通道(multi-channel),regular的訊號 ( signal ) 輸入,相關參數定義詳列如下表。
|
參數名稱 |
參數定義 |
預設值 |
|
Stats Mode |
如果輸入訊號為多通道,此參數將會被開啟,包含PerChannel 和 AcrossChannel。 若如預設 PerChannel ,結果會為一個 15 * n 的矩陣,其中 n 為輸入的 channel 數,15 個值為計算的統計值,輸出格式是 Indexed 的數值資料。 若設定為 AcrossChannel,計算同一個時間點下,輸入訊號中所有通道的 15 個統計值,最後輸出一個多通道訊號包含 15 個 channel ,長度跟輸入訊號相同。 |
PerChannel |
|
View Statistics… |
開啟 Reporter 視窗顯示模組元件計算結果。 |
無 |
|
Unbiased Moment Estimation |
如果輸入資料為樣本 (Sample),則選擇 True (Unbiased Moment Estimation) 進行統計量修正,進一步去推估母體 (Population) 的統計量。 反之若資料為母體 (Population),即可以設定 False ( biased Moment Estimation ),計算母體統計量 |
True |
|
Trimmed Fraction |
截頭尾平均的截去比例,以百分比表示%。 |
0.05 |
|
Trimmed at Ceiling |
當截去比例下之資料點位置為小數點時,選擇取前一點(參數設為 False )或是後一點(參數設為 True )作為 Trimmed 的點數。 |
False |
範例(Example)
計算白色雜訊與方波的基本統計分析:
-
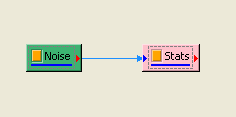
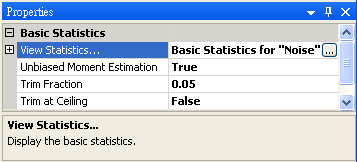
於 Network 視窗下選擇 Source / Noise 創造一個雜訊(預設為白色雜訊),後接上 Compute / Statistics / Basic Statistics,再點選 Basic Statistics 的 Properties / View Statistics…顯示計算結果。
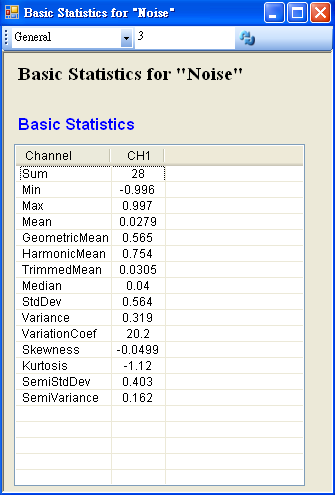
-
另新增一正弦波,用 Conversion / Merge to multi-channel 將此波與 Noise 結合為 Multi-channel 訊號,先以 Viewer / Channel viewer 繪製結果,再拉入 Stats,點選 Basic Statistics 的 Properties / ViewStatistics…,Basic Statistics 視窗即更新如下。
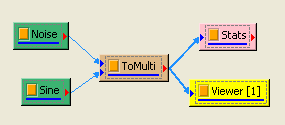
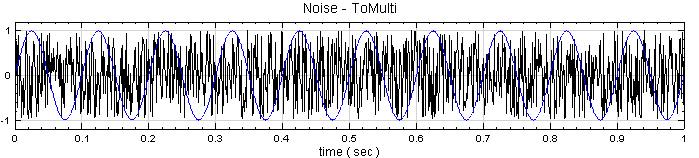
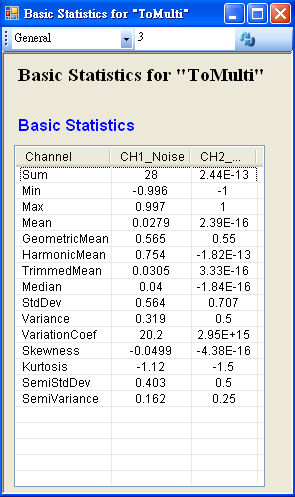
-
設定 Basic Statistics 工具列上的參數,使數值顯示為 Scientific,小數點位數調整為 5 位,最後記得按 Refresh 鈕更新,其結果顯示如下。
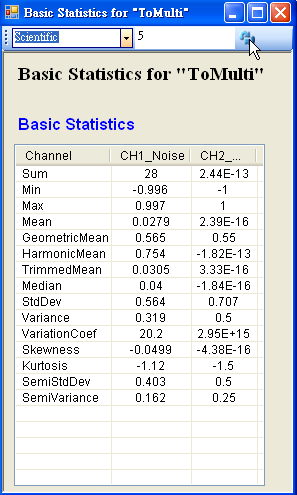
-
另外在一個新的專案中,Source / Noise 產生一個 White Noise,再將其接至 HHT / RCADA EEMD,最後以 Channel Viewer 觀看其結果。

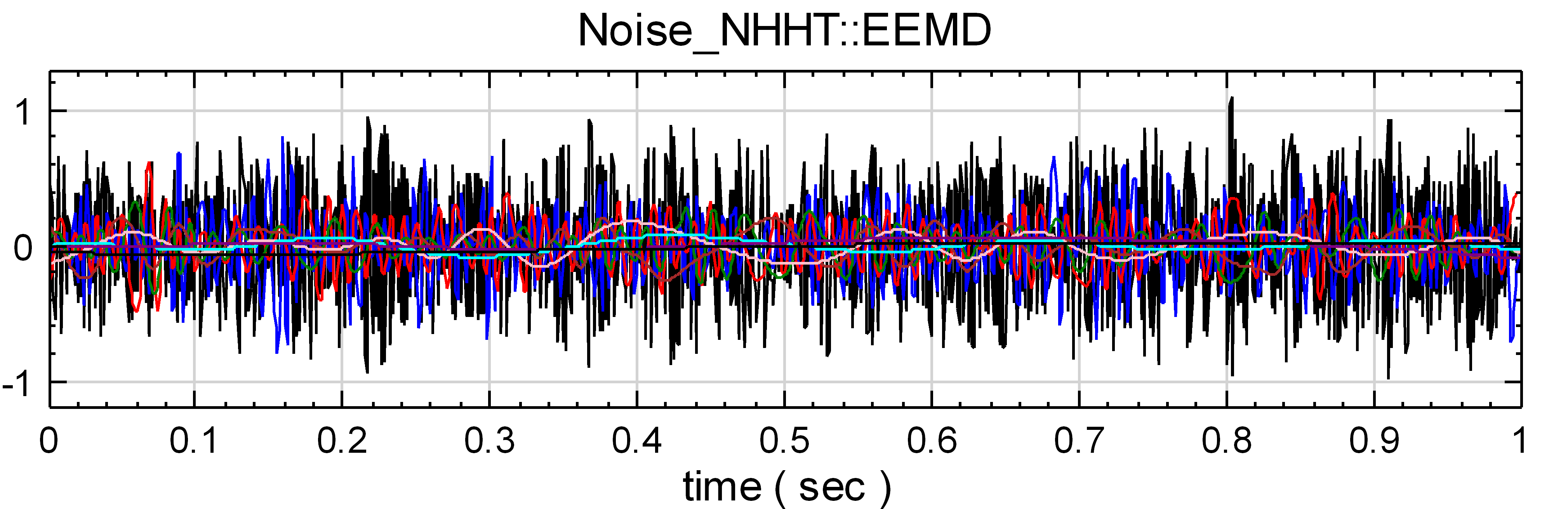
-
最後再將 RCADA EEMD 連接至 Compute / Statistics / Basic Statistics,然後 Properties / Stats Mode 選擇 AcrossChannels, 最後以連接 Compute / Channel / Channel Switch, Channel Viewer觀看其結果,可以利用 Channel Switch 選擇不同通道,檢視不同的統計量。
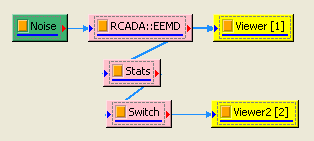
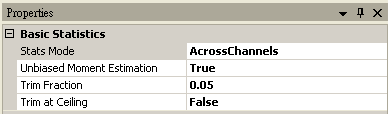
相關指令
Equiphase Statistics,Rolling Statistics,Merge to Multi。
參考
Michel Loeve, "Probability Theory", Graduate Texts in Mathematics, Volume 45, 4th edition, Springer-Verlaf, 1977
Joanes, D. N.&Gill, C. A.(1998) Comparing measuresof sample skewness and kurtosis. Journal of the Royal Statistical Society (Series D): The Statistician 47 (1), 183–189.
共變異數是計算兩組數列各自對其平均值的變化相關程度,若值為正,代表兩數列呈正相關,值為負代表兩數列呈負相關。倘若有多比數列資料互相比較,則可將各資料對應之共變異數組成一個共變異數矩陣。
說明
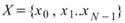 ,
,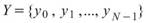 為兩組數列,則總量之共變異數(Covariance)計算如下:
為兩組數列,則總量之共變異數(Covariance)計算如下:
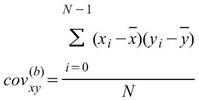
其中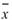 、
、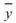 分別為兩數列的平均值。若考慮樣本不偏估之估計量(Unbiased
estimator),則方程式為
分別為兩數列的平均值。若考慮樣本不偏估之估計量(Unbiased
estimator),則方程式為
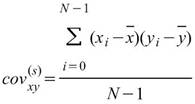
若有一組多通道(multi-channel)的數列,通道數為 M,則各通道間對應的總量/樣本相關係數可表示為共變異數矩陣。
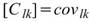 ,其中 l,k 為數列通道編號。
,其中 l,k 為數列通道編號。
其中矩陣的對角項(Diagonal terms)就是該通道數列的變異數,即:
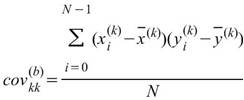
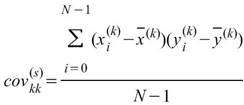
參數設定(Properties)
本模組接受實數(real number),多通道(multi-channel),regular 的訊號 ( signal ) 輸入。輸出為一個 M x M 的方形矩陣,其中 M 為通道數,輸出格式是 Indexed 的數值資料。計算結果於 Properties / View Matrix… 即可開啟 Reporter 視窗看到。
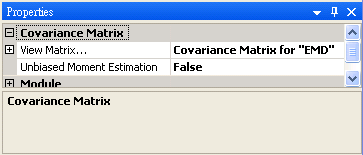
參數為 Unbiased Moment Estimation,可選擇是否計算樣本不偏估之共變異數矩陣,預設為“False”。
範例(Example)
以不同相位角與頻率的正弦波為輸入訊號計算其相關係數矩陣:
-
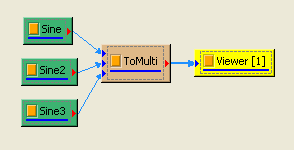
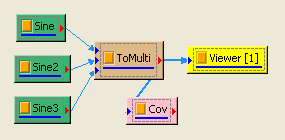
於 Network 視窗下按右鍵,選擇Source / Sine Wave 創造一個正弦波,此波預設頻率為 10Hz,接著再創造兩個正弦波,一個波設定其 Properties / SignalFreq = 5Hz,另一個波設定其 Properties / Phase=180 度(單位為Degree),最後使用 Conversion / Merge to Multi-channel 將三個訊號結合成一個 Multi-Channel 的訊號。以上步驟將創造一個頻率為 10Hz 的正弦波,頻率為 5Hz 的正弦波以及相位角偏移 180 度 的正弦波。以Viewer / Channel Viewer 繪出結果,其中黑線代表Sine,藍線代表 Sine2,紅線代表 Sine3。
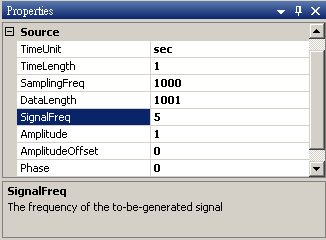
Sine2 的參數設定如下圖。
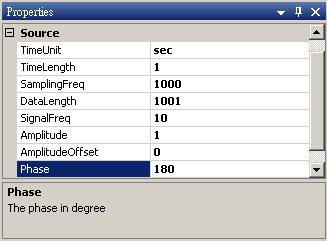
Sine3 Properties
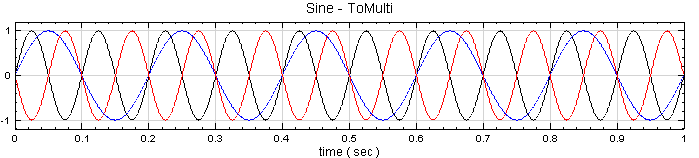
-
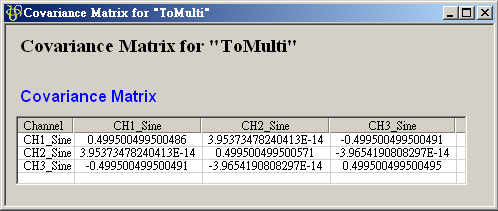
在 ToMulti 後方接上 Compute / Statistics / Covariance Matrix,點選其 Properties / View Matrix… 跳出計算結果。矩陣元素
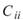 為各訊號對自己的共變異數,也就是各訊號的變異數約
0.499,
為各訊號對自己的共變異數,也就是各訊號的變異數約
0.499,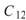 、
、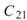 是 Sine 與 Sine2
的比較,其值極小,表示兩訊號無相關性,
是 Sine 與 Sine2
的比較,其值極小,表示兩訊號無相關性,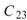 、
、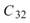 同樣為極小值,同理 Sine與 Sine2
也是無相關性;Sine 與 Sine3 為與 X 軸對稱的兩數列,其計算結果為 -0.499,代表兩訊號為負相關。
同樣為極小值,同理 Sine與 Sine2
也是無相關性;Sine 與 Sine3 為與 X 軸對稱的兩數列,其計算結果為 -0.499,代表兩訊號為負相關。
-
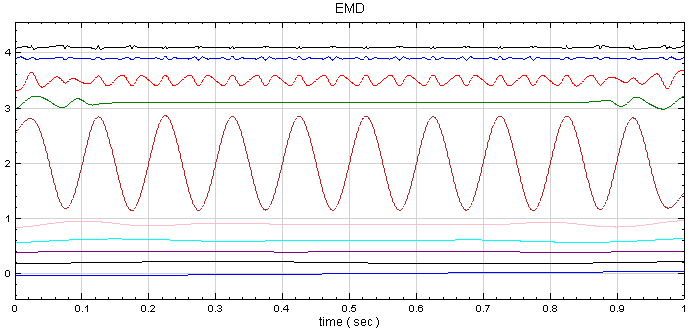
再開一個新的專案,以 Source / Triangle Wave 產生一組三角波,再接上 Compute / HHT / RCADA EEMD 計算出三角波的 IMF,計算結果以 Channel Viewer 繪出。Viewer 的 Properties / Multi-channel Display 調為 List,Viewer Height 調為 350,可以看到共分出 10 個通道的訊號。
-
於 RCADAEEMD 後面再接上Compute / Statistics / Covariance Matrix,計算各 IMF 之間的共變異數矩陣。
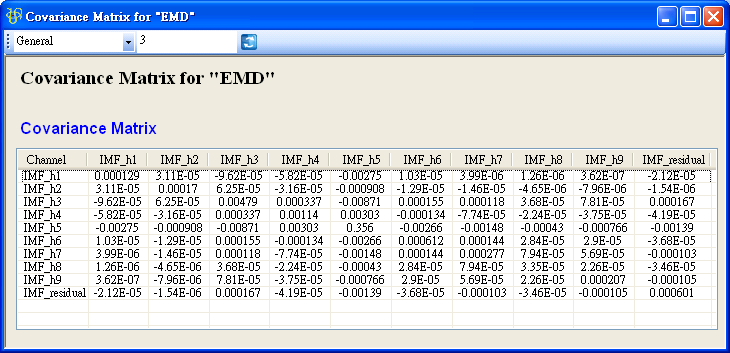
共變異數值的大小可衡量兩數列值變化的程度,值為正代表兩數列值相對於平均的變化趨勢相同,為正的線性相關,值為負代表兩數列值相對於平均的變化趨勢相反,為負的線性相關。另外可注意到矩陣的對角項為各通道的變異數。
相關指令
Correlation Matrix,Orthogonality Matrix,Merge To Multi-Channel,RCADA EEMD。
參考
N.G. van Kampen, Stochastic processes in physics and chemistry. New York: North-Holland, 1981.
相關係數(Correlation Coefficient)即是正規化的共變異數,可指出兩組數列的相關程度,倘若有多筆數列相互交差比較,則可將各相關係數組成相關係數矩陣。
說明
令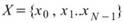 ,
,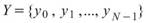 為兩組數列,則相關係數(Correlation
Coefficient)之計算如下:
為兩組數列,則相關係數(Correlation
Coefficient)之計算如下:
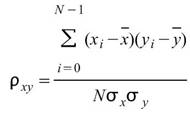
其中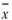 、
、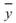 分別為兩數列的平均值,
分別為兩數列的平均值,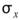 、
、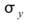 分別為兩數列的標準偏差。若考慮樣本不偏估之估計量(Unbiased
Moment estimator),則方程式為
分別為兩數列的標準偏差。若考慮樣本不偏估之估計量(Unbiased
Moment estimator),則方程式為
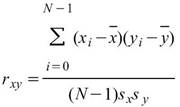
其中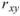 為兩樣本數列的相關係數,
為兩樣本數列的相關係數,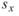 、
、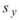 分別為兩數列的樣本標準偏差。相關係數之定義可視為共變異數除以兩數列之標準偏差。若有一組多通道(multi-channel)的數列,通道數為
M,則各通道間對應的總量 / 樣本相關係數可表示為相關係數矩陣。
分別為兩數列的樣本標準偏差。相關係數之定義可視為共變異數除以兩數列之標準偏差。若有一組多通道(multi-channel)的數列,通道數為
M,則各通道間對應的總量 / 樣本相關係數可表示為相關係數矩陣。

其中l,k 為通道代碼。
參數設定(Properties)
本模組接受實數(real number),多通道(multi-channel),regular的訊號(signal)輸入。輸出為一個 M x M 的方形矩陣,M 為channel數,輸出格式是 Indexed 的數值資料。於 Properties / View Matrix… 即可用Reporter視窗看到計算結果。
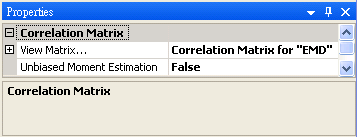
參數為 Unbiased Moment Estimation,可選擇是否計算樣本不偏估之相關係數矩陣,預設為 " False "。
範例(Example)
以不同相位角與頻率的正弦波為輸入訊號計算其相關係數矩陣結果:
-
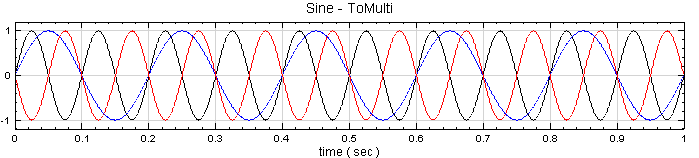
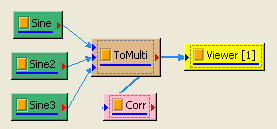
於 Network 視窗下按右鍵,選擇 Source / Sine Wave 創造一個正弦波,此波預設頻率為 10Hz,接著再創造兩個正弦波,一個波設定其Properties / SignalFreq = 5Hz,另一個波設定其 Properties / Phase = 180 度(單位為Degree),最後使用 Conversion/Merge to Multi-channel 將三個波結合成一個 Multi-Channel 的訊號。以上步驟將創造一個頻率為 10Hz 的正弦波,頻率為 5Hz 的正弦波以及相位角偏移 180 度的正弦波。以 Viewer / Channel Viewer 繪出結果,其中黑線代表Sine,藍線代表Sine2,紅線代表Sine3。
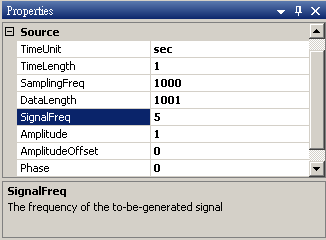
Sine2 Properties
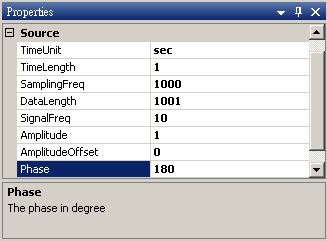
Sine3 Properties
-
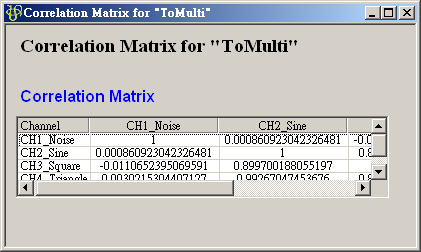
在 ToMulti 後方接上 Compute / Statistics / Correlation Matrix,點選其 Properties / View Matrix… 跳出計算結果。矩陣對角項
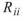 為各訊號對自己的相關係數,因此為 1
完全相關,
為各訊號對自己的相關係數,因此為 1
完全相關,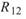 、
、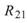 是 Sine 與 Sine2
的比較,其值約為
是 Sine 與 Sine2
的比較,其值約為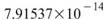 ,表示兩訊號無相關性,
,表示兩訊號無相關性,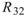 、
、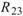 同樣為極小值,同理 Sine 與 Sine2
也是無相關性;Sine 與 Sine3 為與x軸對稱的兩數列,其計算結果為 -1,代表完全負相關。
同樣為極小值,同理 Sine 與 Sine2
也是無相關性;Sine 與 Sine3 為與x軸對稱的兩數列,其計算結果為 -1,代表完全負相關。
-
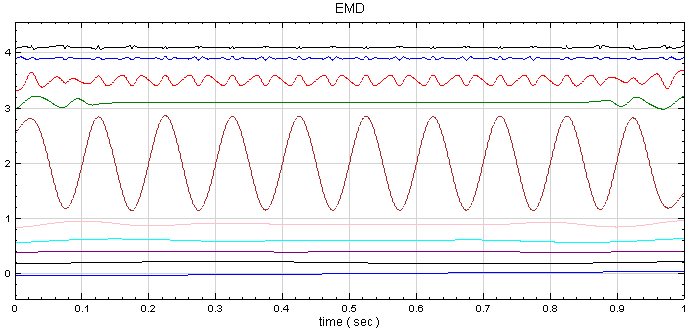
再開一個新的專案,以 Source / Triangle Wave 產生一組三角波,再接上 Compute / HHT / RCADA EMD 計算出三角波的 IMF,計算結果以 Channel Viewer 繪出。Viewer 的 Properties / Multi-channel Display 調為 List,Viewer Height 調為 350,可以看到共分出 10 個通道的訊號。

-
於 RCADA EMD 後面再接上出 Compute / Statistics / Correlation Matrix,這樣可計算出各 IMF 之間的相關係數。
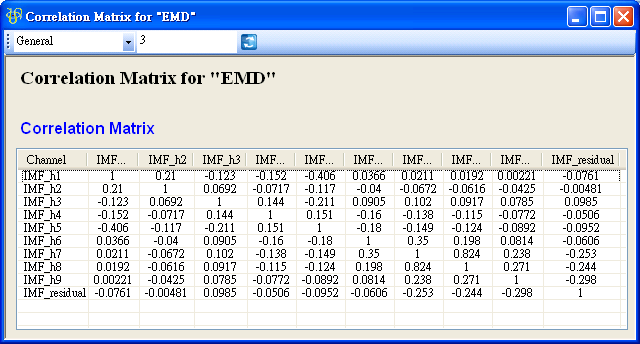
矩陣的對角項為各通道對自己的相關係數,所以等於 1;除了對角項之外,值最大的相關係數為 IMF_h5 與 IMF_h1,表示這兩組訊號有較強的相關性,其餘大多數的相關係數值都小於正負 0.1,代表其餘 IMF 彼此間的相關性很小。
相關指令
Covariance Matrix,OrthogonalityMatrix,Merge To Multi-Channel,Channel Viewer,RCADA EMD。
參考
Cohen, J., Cohen P., West, S.G.,&Aiken, L.S. (2003). Applied multiple regression/correlation analysis forthe behavioral sciences. (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associmtes.
等相位統計值,為設定一段長度為 M 的週期,在此週期下計算每個同相位元素的統計值,譬如計算月均值,週均值等,此計算方式即為 Equiphase Statistics。
說明
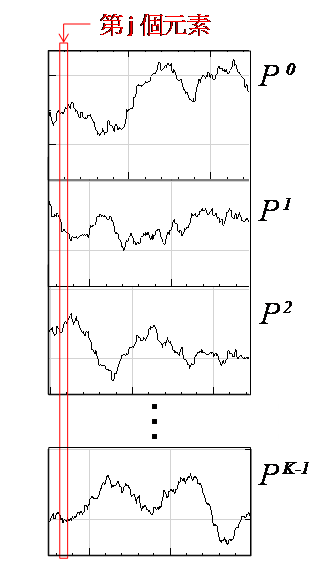
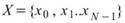 為一組個數為 N 的數列,而 Equiphase
Statistics 所設定的週期大小為 M,M<N,則此數列可分作 K = Ceiling ( N / M )
個小數列,Ceiling 表示小數點後無條件進位,令小數列為
為一組個數為 N 的數列,而 Equiphase
Statistics 所設定的週期大小為 M,M<N,則此數列可分作 K = Ceiling ( N / M )
個小數列,Ceiling 表示小數點後無條件進位,令小數列為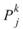 ,k 標示小數列編號,j 標示數列內之元素,則
,k 標示小數列編號,j 標示數列內之元素,則
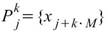 ,
,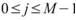 ,
,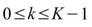 (如下圖所示)
(如下圖所示)

EquiphaseStatistics 就是抽出每個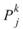 中相同相位的元素作為一組,計算其統計值,譬如
equiphase mean 的計算如下。
中相同相位的元素作為一組,計算其統計值,譬如
equiphase mean 的計算如下。
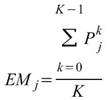 ,
,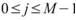 。
。
須注意當 N / M 不整除時,最後一組小數列長度 M_last<N,因此當相位元素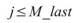 時,計算之元素數量為 K,當元素 j>M_last
時,計算元素數量為 K-1。
時,計算之元素數量為 K,當元素 j>M_last
時,計算元素數量為 K-1。
Equiphase statistics 可計算多種統計值,其中大部份與 Basic statistics 模組相同,此處不再贅述,算式請參照 Basic statistics 內容,其它部份,譬如 First quartile、Third quartile 與 Quantile 的詳細定義請參考 Quartiles and Quantiles 模組。
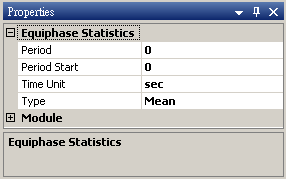
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入。參數定義如下。
|
參數名稱 |
參數定義 |
預設值 |
|
Period |
設定週期,單位為時間。 |
輸入訊號時間總長的百分之十 |
|
Period Start |
設定起始點位置,單位為時間。 |
0 |
|
TimeUnit |
時間單位。 |
sec |
|
Type |
設定要計算的統計量。 |
Mean |
Type選項定義如下,計算於窗內範圍的統計量。
|
選項名稱 |
選項定義 |
|
Sum |
數列總合。 |
|
Min |
數列中最小值。 |
|
Max |
數列中最大值。 |
|
Mean |
平均值。 |
|
Geometric Mean |
幾合平均數。 |
|
Harmonic Mean |
調合平均數。 |
|
Trimmed Mean |
截尾平均數。 |
|
First quartile |
數列值四分位值。 |
|
Median |
數列的中位數。 |
|
Third quartile |
數列的四分之三位值。 |
|
Quantile |
數列的分位數。 |
|
StdDev |
數列的標準偏差。 |
|
Variance |
數列的變異數。 |
|
VarianceCoef |
變異係數。 |
|
Skewness |
數列的偏度。 |
|
Kurtosis |
數列的峰度。 |
|
SemiVariance |
半變異數。 |
|
SemiStdDev |
半標準偏差。 |
部分選項會再出現參數需要設定,Quantile 的參數請參閱 Quartiles and Quantiles 模組說明,其餘統計量的定義請參考模組Basic Statistics內容。
範例(Example)
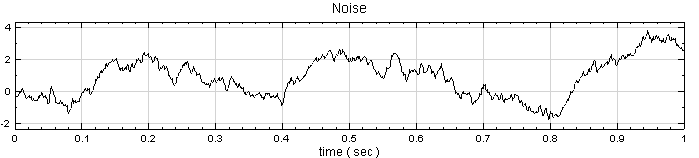
以一組 Brownian Noise 為輸入訊號,計算 Equiphase Statistics 的各項統計值。
-
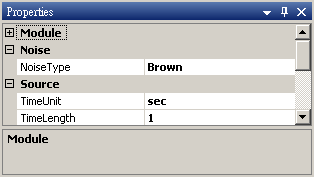
於 Network 按右鍵新增 Source / Noise,調整 Properties / Noise Type 為 Brown,以 Viewer / ChannelViewer 繪出結果。

-
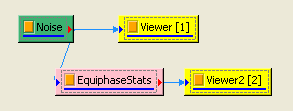
於 Noise後方接 Compute / Statistics / Equiphase Statistics,其統計值預設為 Mean,調整 Properties / Period 為 0.1,讓它以 0.1秒為週期,計算該週期下每個元素的平均值。最後以 Viewer / Channel Viewer 輸出結果。
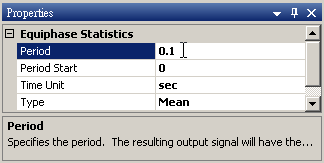
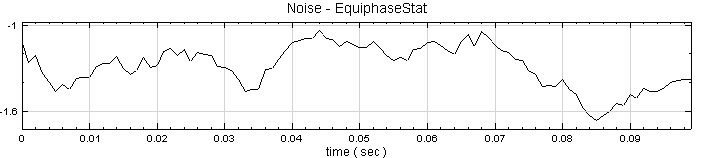
-
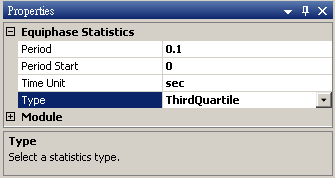
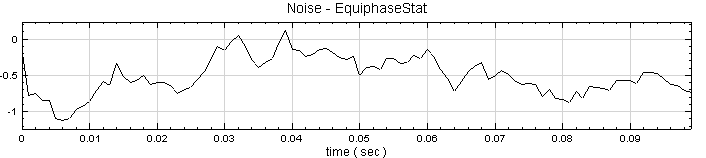
調整 Type 為 Third Quartile,則模組會計算週期下每個元素位置的四分之三位值。
相關指令
Basic Statistics,Rolling Statistics,Quartilesand Quantiles, Channel Viewer。
參考
1. Michel Loeve, "Probability Theory", Graduate Texts in Mathematics, Volume 45, 4th edition, Springer-Verlaf, 1977
2. Joanes, D. N.&Gill, C. A. (1998)Comparing measures on sampleskewness and kurtosis. Journal of the Royal Statistical Society (Series D): The Statistician 47 (1), 183–189.
Kernel smoothing density estimation 是以非參數化(non-parametric)的方法計算出數列的機率密度函數( probability density function )。
說明
設數列為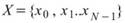 ,則數列的 kernel density
estimation 為:
,則數列的 kernel density
estimation 為:
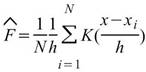
其中 h 是控制平滑程度的參數,即平滑窗 ( smoothing window ) 的長度,K 是核函數 ( kernel function )。此方法是將離散分佈之每個點代入核函數中,再疊加每個點的核函數計算結果,以達到平滑之目地。在概念上與作統計直方圖類似。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)輸入;輸出訊號格式為實數,多通道,regular的訊號。
參數定義整理如下表。須注意 KS Density 輸出的訊號格式,一組輸入訊號會產生一組兩個通道的輸出訊號,第一個通道為 X 軸資料,以資料的極大及極小為上下界限,第二個通道為 Y 軸資料,為數列數值相對應之機率密度值。
|
參數名稱 |
參數定義 |
預設值 |
|
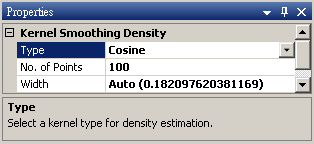
Type |
核函數的種類,內建函數包括Uniform、Triangle、Epanechnikov、Quartic、Triweight、Gaussian、Cosine,其定義整理至下一個表格中。 |
Gaussian |
|
No. of Points |
輸出訊號之離散點數。 |
100 |
|
Width |
平滑窗之寬度, 即 h,為控制平滑程度的常數,預設值 Auto 是假設標準常態分佈下計算最佳的寬度。 |
Auto |
下表整理常見核函數之定義。
|
核函數名稱 |
定義 |
|
Uniform |
|
|
Triangle |
|
|
Epanechnikov |
|
|
Quartic |
|
|
Triweight |
|
|
Gaussian |
|
|
Cosine |
|
範例(Example)
-
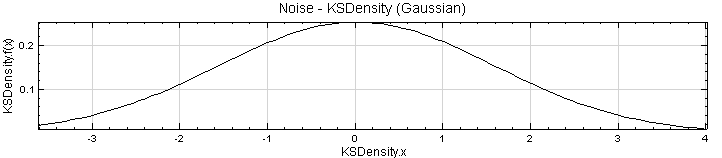
建立一個 Source / Noise,調整其 Properties/Noise Type 為 Gaussian,Time Length 設為 10 秒,再接上 Kernel Smooth Density,連結上 XY Plot。
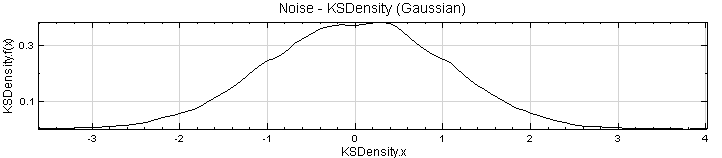
-
另一方面將 Noise 直接以 Viewer / Histogram Viewer 繪出,將 Histogram 的 Properties / BinCount 調整為 50,Percentage 調為 True,則可畫出下面的直方圖。
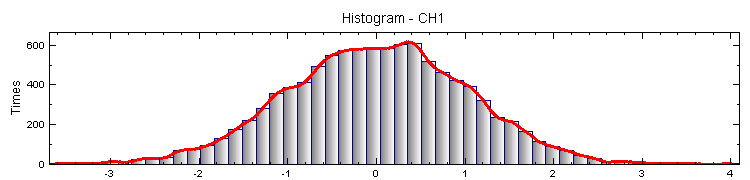
這兩張圖的基本概念是相同的,kernel smooth density 是以 kernel function 將數值出現的機率轉為連續的密度函數表示,而 histogram 是以值區間計算每個區間內數值發生的機率;且本模組所計算的密度函數其 X 軸以上的面積為 1,而 histogram 的 Y軸直接是發生次數。
將 KSDensity 的 Properties / Width 調大一點,調整到 1.2,可看到結果更為平順。
相關指令
Histogram,Noise,XY Plot。
參考
T. Hastie, R. Tibshirani and J. Friedman, The Elements of Stbtistical Learning, Chapter 6, Springer, 2001.
正交性矩陣是計算數列間的正規化的內積 ( Dot Product ),若兩訊號正交,則其值為零,可以用在 EMD 計算的 IMF 上,判斷各 IMF 彼此間是否正交。
說明
令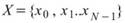 ,
,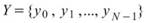 為兩組數列,則其正交性定義為兩數列的內積,計算如下:
為兩組數列,則其正交性定義為兩數列的內積,計算如下:
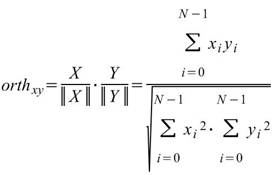
若有 M組數列,與其對應的正交性矩陣表示如下:
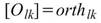 ,其中 l,k 為通道編號。
,其中 l,k 為通道編號。
參數設定(Properties)
本模組接受實數(real number),多通道(multi-channel),regular的訊號(signal)輸入。輸出為一個 M x M 的方形矩陣,M 為輸入訊號的通道數,輸出格式是Indexed的數值資料。於Properties/View Matrix…即可用Reporter視窗看到計算結果。
範例(Example)
以不同相位角與頻率的正弦波為輸入訊號計算,正交性矩陣:
-
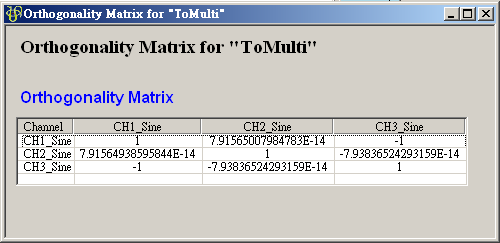
於 Network 視窗下按右鍵,選擇 Source / Sine Wave 創造一個正弦波,此波預設頻率為 10 Hz,接著再創造兩個正弦波,一個波設定其Properties / SignalFreq = 5Hz,另一個波設定其 Properties / Phase =180 度(單位為Degree),最後使用 Conversion / Merge to Multi-channel 將三個波結合成一個 Multi-Channel 的訊號。以上步驟將創造一個頻率為10Hz 的正弦波,頻率為 5Hz 的正弦波以及相位角偏移 180 度的正弦波。以 Viewer/ Channel Viewer 繪出結果,其中黑線代表Sine,藍線代表Sine2,紅線代表Sine3。
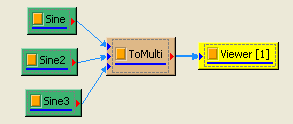
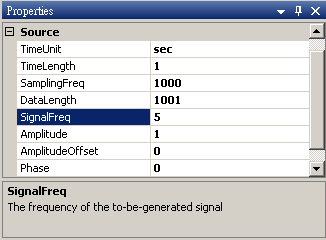
Sine2 Properties
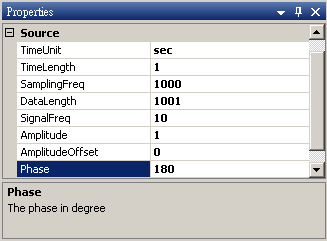
Sine3 Properties
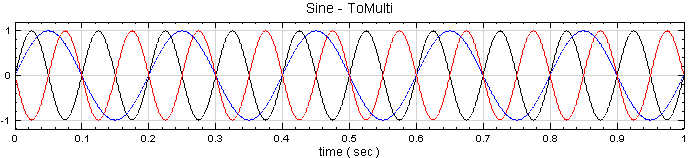
-
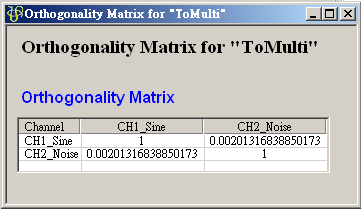
在 ToMulti 後方接上 Compute / Statistics / Orthogonality Matrix,點選其 Properties / View Matrix…跳出計算結果。矩陣對角項
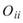 為各訊號對自己的正交性,也就是訊號對自己作內積,其值為1;
為各訊號對自己的正交性,也就是訊號對自己作內積,其值為1;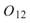 、
、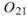 是
Sine 與 Sine2 的比較,其值極小,表示兩訊號相互正交,
是
Sine 與 Sine2 的比較,其值極小,表示兩訊號相互正交,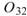 、
、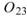 同樣為極小值,同理 Sine 與 Sine2
也是相互正交;Sine 與 Sine3 為對 X 軸對稱的兩數列,因此其計算結果為 -1。
同樣為極小值,同理 Sine 與 Sine2
也是相互正交;Sine 與 Sine3 為對 X 軸對稱的兩數列,因此其計算結果為 -1。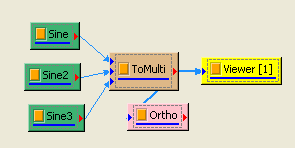

相關指令
Covariance Matrix,Correlation Matrix,Merge To Multi-Channel,Channel Viewer。
參考
Probability, Random Variables and Stochastic Processes. McGraw-Hill, 211.
四分位數與分位數。分位數為一數列經排序後,其分佈位置占總量某個百分比的數值,而四分位數是在總量25%、50%、75%的位置的數值。
說明
令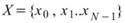 為一組個數為N的數列,則四分位數可表示為
為一組個數為N的數列,則四分位數可表示為
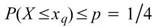 ,
,
若以較明確的說法,一數列的四分位數是其累積分佈函數等於 25% 的數值,位置 q 在 N * 25% - 1 處,中位數與四分之三位數也是相同的概念。分位數 Quantile 則是更一般化的分位數,以百分比為標準,如 17 位數(17thquantile) 代表在數列中累積分佈函數等於17%的數值。
若估計分位數時,該分位位置在兩點之間(即 q = N * p - 1 不為整數),則需要推估該分位的位置,估計方法眾多,本元件整理五種較常用的計算式供使用者選擇。
|
內插方法 |
定義 |
說明 |
|
Linear |
其中 i 代表 q 的整數部分 |
分位位置的前一點與下一點的數值作線性內插計算分位數。 |
|
Next point |
|
以分位位置下一點的數值當作分位數。 |
|
Average |
|
分位位置的前一點與下一點的數值取平均作為該分位數。 |
|
Weighted Average |
其中 i 是 ( N-1 ) * p 的整數部份,g 是小數部份。 |
分位位置的前一點加上前後兩點之差的加權值,此方法被Microsoft Office Excel 所採用。 |
|
Nearest |
其中 i 是 ( N-1 ) * p 的整數部份,g 是小數部份。 |
離分位位置最近的位置作分位數。 |
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)輸入。
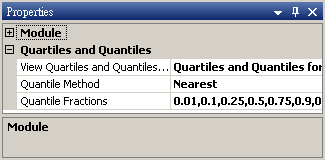
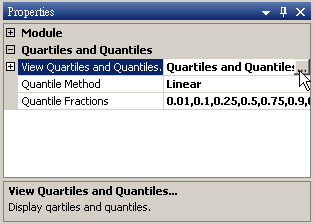
參數設定介面如下圖,本模組預設就計算數列的四分位數、中位數、四分之三位數等 Quartiles 值,另外可在參數 Quantile Fractions 下設定希望計算的 Quantiles 值。參數View Quartiles and Quantiles…會跳出視窗顯示計算結果。參數 Quantile Method 則可選擇 Quantile 的估計方法。下面就各參數內容分項說明。
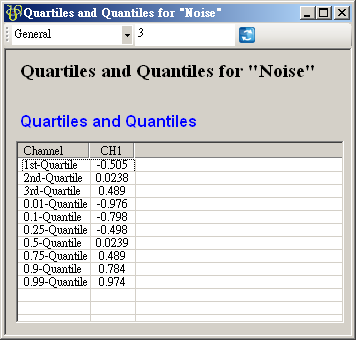
上圖為按下 View Quartiles and Quantiles… 右方![]() 鈕即跳出視窗,每一筆訊號的計算結果以 Column 為單位呈現,第一個 Column 顯示 Quartile
與 Quantile 名稱,第二 Column 之後每個 Column 都對應至輸入訊號每個 Channel,前三 Rows
計算三個四分位值,後面的 Rows 計算Quartiles,使用者利用參數 Quartile Fractions
來設定。下面將介紹參數 Quantile Fractions。
鈕即跳出視窗,每一筆訊號的計算結果以 Column 為單位呈現,第一個 Column 顯示 Quartile
與 Quantile 名稱,第二 Column 之後每個 Column 都對應至輸入訊號每個 Channel,前三 Rows
計算三個四分位值,後面的 Rows 計算Quartiles,使用者利用參數 Quartile Fractions
來設定。下面將介紹參數 Quantile Fractions。
Quantile Fractions 有兩種方式可以設定分位數。第一種方法是直接在欄位裡更改數據,譬如在0.1與0.25之間鍵入「0.2,」(如下圖),就可以新增分位數。
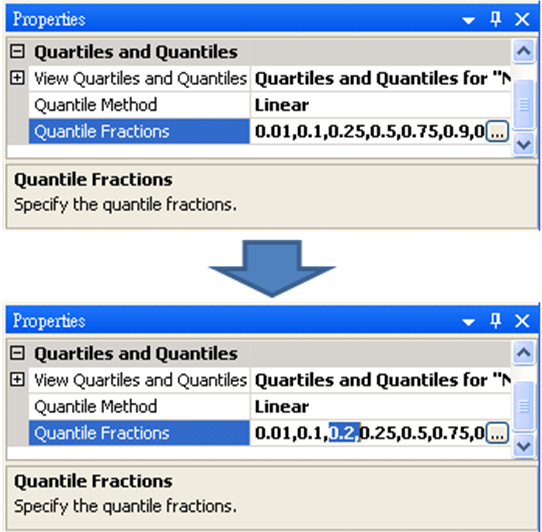
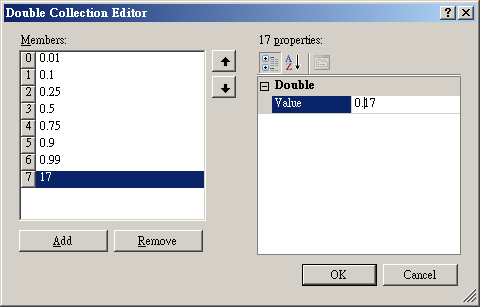
第二種方法是按下 Quantile Fractions 右方![]() 鈕,跳出分位數編輯視窗(如下圖),如果一次需要新增或移除很多個分位數,可以採取此作法。左邊為設定的
Quantile Member,使用者可以用下面的 Add / Remove 按鈕新增/移除計算項目,另外可以在右邊視窗編輯每個
Member 要計算的 Quantile 的比例,如 0.01 代表 1% Quantile,編輯完成後,按下 OK
鈕即完成設定。設定後這些 Quantiles 的計算結果會顯示在成 View Quartiles and
Quantiles…視窗中。
鈕,跳出分位數編輯視窗(如下圖),如果一次需要新增或移除很多個分位數,可以採取此作法。左邊為設定的
Quantile Member,使用者可以用下面的 Add / Remove 按鈕新增/移除計算項目,另外可以在右邊視窗編輯每個
Member 要計算的 Quantile 的比例,如 0.01 代表 1% Quantile,編輯完成後,按下 OK
鈕即完成設定。設定後這些 Quantiles 的計算結果會顯示在成 View Quartiles and
Quantiles…視窗中。
Quantile Method 內有五種方法,分別為 linear、next、mean、weighted mean、nearest,其估計原理在理論中都有詳述。
|
參數名稱 |
參數定義 |
預設值 |
|
View Quartiles and Quantiles |
顯示計算的 Quartiles 和 Quantiles結果。 |
無 |
|
Quantile Method |
Linear、Next、Mean、Weighted mean、Nearest。 |
Linear |
|
Quantile Fractions |
可設定多個 Quantile 的百分比。 |
[0.01; 0.1; 0.25; 0.5; 0.75; 0.9; 0.99] |
範例(Example)
以一組Brownian Noise為輸入訊號,計算 Quartiles 與 Quantiles。
-
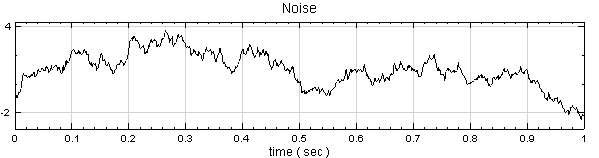
於 Network 按右鍵新增 Source / Noise,調整 Properties / Noise Type 為 Brown,以Viewer / Channel Viewer 繪出結果。
-
於 Noise 後方接 Compute / Statistics / Quartiles and Quantiles 計算各項分位數值,點擊 Properties / View Quartiles and Quantiles…檢視結果。
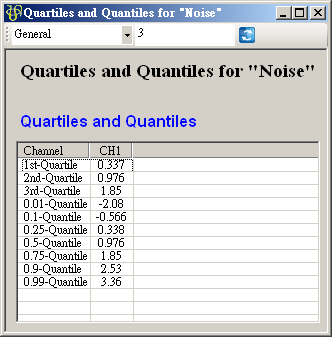
-
點選 Properties / Quantile Fractions 來編輯不同的分位值,按下編輯介面的 Add 按鈕(如下圖),會在 Members 處新增一個值為 0 的 member。
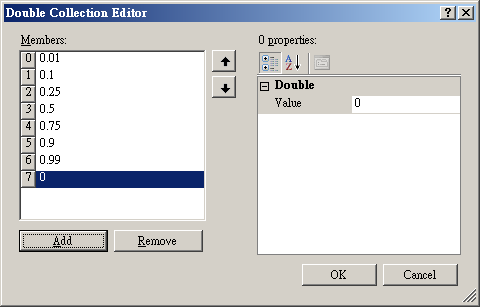
接下來,於編輯介面的右邊可設定分位數的百分比,譬如說設定為 0.17,完成後按下 OK 鈕。
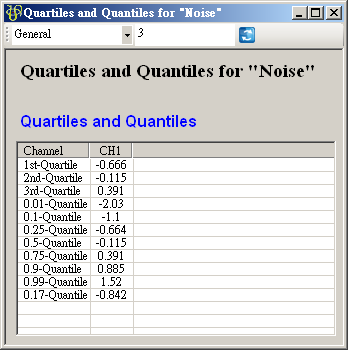
-
再次點選 View Quartiles and Quantiles…,可以看到已經新增了一個 17th Quantile。
相關指令
Basic Statistics,Rolling Statistics,Channel Viewer。
滾動統計值,為設定一段元素數量為 M 的窗,統計函數計算窗內部份的統計值,譬如平均值,並且移動此窗以計算出的新的數列,此計算方式即為 Rolling statistics。
說明
令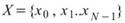 為一組個數為 N 的數列,而 rolling
statistics 所設定的窗
為一組個數為 N 的數列,而 rolling
statistics 所設定的窗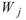 長度為
M,M<N,則此窗內的元素可表示為
長度為
M,M<N,則此窗內的元素可表示為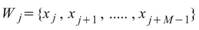 ,其中
,其中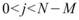 ,Rolling statistics
就是計算此窗內的統計值,譬如 Rolling mean
,Rolling statistics
就是計算此窗內的統計值,譬如 Rolling mean
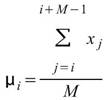 ,
,![]() 。
。
另外定義一個 overlap 值 ( p ) ,p 代表計算下一段窗時,有多少窗內的元素是與前一段重疊的。以 rolling means 為例,設定窗大小 M = 10,則輸出值第一點
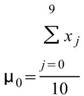 , 即下圖
, 即下圖
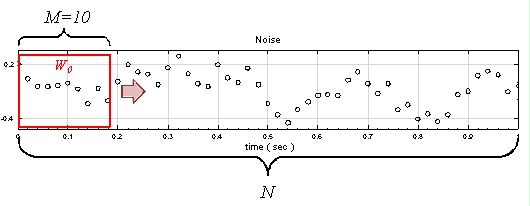
範圍是訊號位置 0 至 9 ,如上圖所示,若 p = 9,則計算下一段窗的範圍是在訊號位置 1至 10處,即
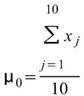
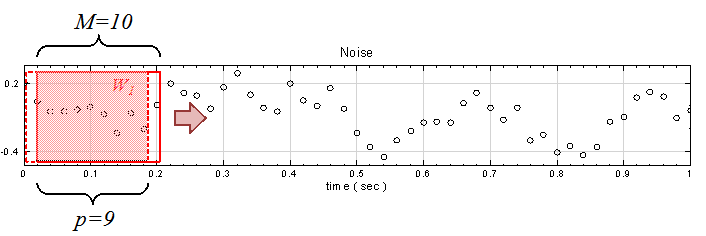
兩段相比有 9 個位置重疊。倘若 p = 7,則
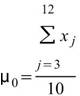 ,
,
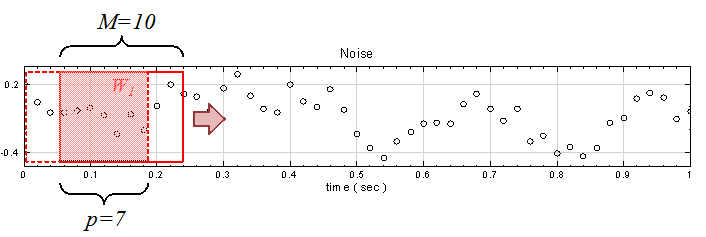
與前段相比有 7 個訊號位置重疊,以此類推,輸出數列的長度為
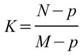 ,
,
須注意當 m - p>1 時,輸出數列的長度 K 可能無法整除的狀況,而處理方式為捨去餘數,僅保留完整的窗所計算的結果,因此
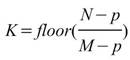 。
。
Rolling statistics 可計算某種統計值,項目與 Basic statistics 模組相同,此處不再贅述。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)輸入。參數定義如下。

|
參數名稱 |
參數定義 |
預設值 |
|
Type |
可選擇想要計算的統計值,詳細清單可見下表。 |
Mean |
|
Window |
設定窗的大小,單位為訊號元素個數。 |
2 |
|
Overlap |
設定rolling時重疊元素的數量。 |
Window -1 |
Type選項定義如下,計算於窗內範圍的統計量。
|
選項名稱 |
選項定義 |
|
Sum |
計算總合。 |
|
Min |
數列中最小值。 |
|
Max |
數列中最大值。 |
|
Mean |
平均值。 |
|
Geometric Mean |
幾合平均數。 |
|
Harmonic Mean |
調合平均數。 |
|
Trimmed Mean |
截頭尾平均數。 |
|
First quartile |
數列的四分位值。 |
|
Median |
數列的中位數。 |
|
Third quartile |
數列的四分之三分位值。 |
|
Quantile |
數列的分位數。 |
|
StdDev |
數列的標準偏差。 |
|
Variance |
數列的變異數。 |
|
VarianceCoef |
變異係數。 |
|
Skewness |
數列的偏度。 |
|
Kurtosis |
數列的峰度。 |
|
Semivariance |
半變異數。 |
|
SemiStdDev |
半標準偏差。 |
部分選項會再出現參數需要設定,Trimmed Mean 請參考 Basic Statistics 說明文件,Quantile 的參數請參閱 Quartiles and Quantiles 說明文件,其餘統計量的定義請參考模組 Basic Statistics 內容。
範例(Example)
以一組 Brownian Noise 為輸入訊號,計算 rolling statistics 的各項統計值。
-
於 Network 按右鍵新增 Source / Noise,調整 Properties / Noise Type 為 Brown,以 Viewer / Channel Viewer 繪出結果。

-
於 Noise 後方接 Compute / Statistics / Rolling Statistics,其統計值預設為 Mean,window 預設為 2。以 Channel Viewer 輸出結果。

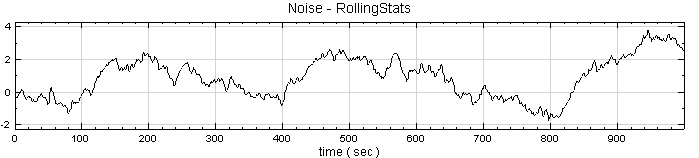
-
因為 window = 2,所以步驟2之計算結果與原訊號差異不大,調整 window 大小為 50,算出的結果如下圖所示;再點選 RollingStats 圖示,按 Network 工具列上 Data Viewer 功能看 Data count 長度,長度為 952,可套用理論中 K 值驗算。
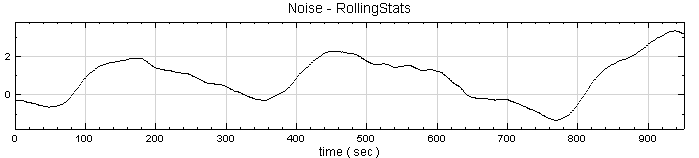
相關指令
Basic Statistics,Equiphase Statistics,Quartiles and Quantiles,Merge To Multi-Channel,Channel Viewer。
先針對母體做出一個適當暫時性假設,再依據隨機樣本統計量的抽樣分配,定義出一個拒絕假設的標準,如果樣本統計量計算後落在拒絕區,則推翻原先建立之暫時性假設,否則必須接受暫時性假設。
理論(Theory)
實驗所得到數據包含機會誤差、真實誤差以及其他影響,利用假設檢定來解決這類問題。一般而言包含三個步驟,設定假設、選擇檢定方法、判斷是否接受假設。
虛無假設 ( Null Hypothesis ) : 實驗數據間的差異屬於機會誤差。
對例假設 ( Alternative Hypothesis ) : 實驗數據間的差異屬於真實誤差。
1. Z-test :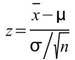
Z-test中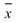 為輸入訊號的平均(樣本平均),
為輸入訊號的平均(樣本平均),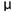 為假設母體平均,
為假設母體平均,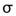 為母體標準差,
為母體標準差,
n 為輸入訊號數量(樣本數量)。
2. T-test :
T-test中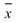 為輸入訊號的平均(樣本平均),
為輸入訊號的平均(樣本平均),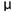 為假設母體平均,
為假設母體平均,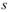 為樣本標準差,n 為輸入訊號數量(樣本數量)。
為樣本標準差,n 為輸入訊號數量(樣本數量)。
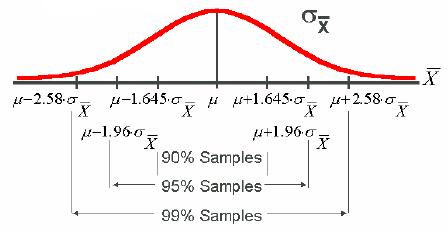
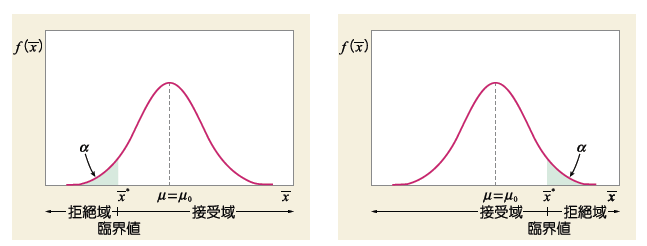
實驗過程中,進行重複相當多次的實驗,實驗結果的平均將會呈現常態分佈 ( 如下圖 ),若要檢驗某次實驗結果是否擁有機會誤差,可以利用Z-test、 T-test,計算出此次實驗平均結果座落常態分佈何處。研究者假設一個拒絕虛無假設範圍,( 以佔常態分佈面積的比例,又稱 Significant Level ),再依照檢定方法 Null (雙尾)、RightTail (右尾) 和 LeftTail (左尾) ( 如下圖 ),判斷實驗平均結果是否落入拒絕範圍。

3.Var-Test (Chi-square variance test) :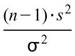
Var-test中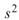 為樣本變異數,
為樣本變異數,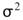 為母體變異數, n 為輸入訊號數量(樣本數量)。
為母體變異數, n 為輸入訊號數量(樣本數量)。
4.Runs-Test ( Runs test of Randomness, Geary test ):
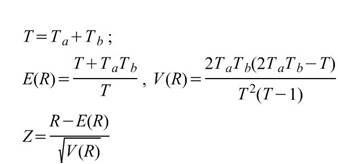
在 Runs-Test 中,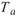 為樣本中大於樣本平均值的數量,
為樣本中大於樣本平均值的數量,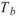 為樣本中小於樣本平均值的數量,R 為由 a , b
的交替出現次數,列如 aaabbaaba,則 R=5。
為樣本中小於樣本平均值的數量,R 為由 a , b
的交替出現次數,列如 aaabbaaba,則 R=5。
參數設定(properties)
Hypothesis Test 目前有四種 One-sample 檢定方法,下面將個別介紹四種檢定方法的參數設定,各參數定義與預設值如下:
|
參數名稱 |
參數定義 |
預設值 |
|
View Test Results |
利用 Hypothesis Test 檢視計算結果。 |
無 |
|
TestType |
z_Test、t_Test、var_Test、runs_Test。 |
z_Test |
如果按下 View Test Result 將會出現檢定結果,顯示結果如下表。
|
參數名稱 |
參數定義 |
|
Rejected |
顯示檢定結果落入拒絕範圍,若顯示 True,表示可以反對虛無假設,反之則只能接受假設。 |
|
SignificanceLevel |
顯示輸入資料平均值落在母體分佈何處。 |
|
CI-Low |
虛無假設的範圍的最小值,也是信賴區間的最小值。 |
|
CI-High |
虛無假設的範圍的最大值,也是信賴區間的最大值。 |
|
Run Count |
參考理論(Theory),此值顯示即為 Runs-Test 的 R。 |
|
Above Threshold |
資料中大於設定門檻的數量。 |
|
Below Threshold |
資料中小於設定門檻的數量。 |
|
z-Value |
此結果只出現在 Runs-Test 中,表示計算出的 Z 值。 |
Z-Test
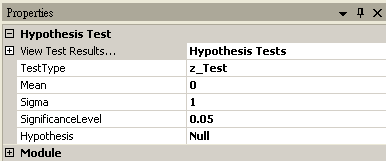
|
參數名稱 |
參數定義 |
預設值 |
|
Mean |
設定母體的平均值。 |
0 |
|
Sigma |
設定母體的標準差。 |
1 |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例。一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為 Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
T-Test
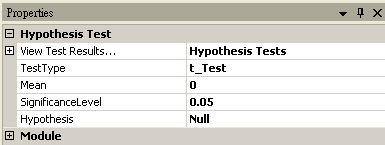
|
參數名稱 |
參數定義 |
預設值 |
|
Mean |
設定母體的平均值。 |
0 |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例,一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為 Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
Var-Test
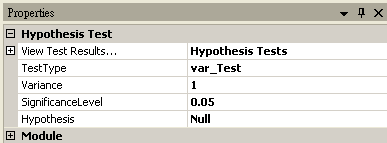
|
參數名稱 |
參數定義 |
預設值 |
|
Variance |
設定母體的變異數。 |
0 |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例,一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為 Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
Runs-Test
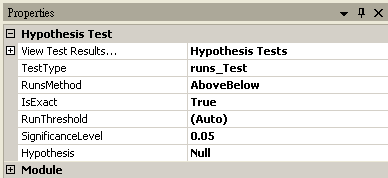
|
參數名稱 |
參數定義 |
預設值 |
|
RunsMethod |
AboveBelow,UpDown。 |
AboveBelow |
|
IsExact |
計算 P-Value 是否用正確的演算法,此參數只存在 RunsMethod = AboveBelow。 |
True |
|
RunThreshold |
設定門檻,決定資料是否大於小於門檻,如果為(Auto),則是輸入資料的平均值。 |
(Auto) |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例,一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
範例(Example)
本範例將舉出幾個範例,解釋各種檢定方法的使用。
-
假設一個秤重儀器,儀器釋格指出無載重時,平均重量為 0.0,標準差為 0.03,每次做實驗之前,需要經校正,利用無秤重時,讀取其顯示重量值,假設讀取 1001 次資料,利用這些資料判斷其儀器是否有偏差,首先虛無假設為儀器無偏差,進行 z-test 檢定。
-
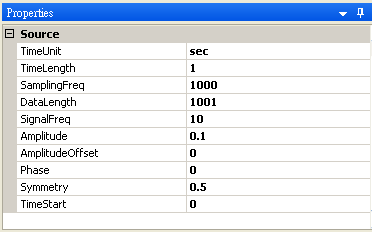
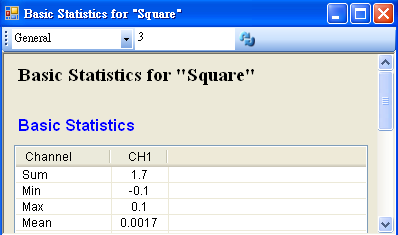
首先以 Source / Square 產生一組量測磅秤的資料,Amplitude 設定為 0.1,再連接至 Compute / Statistics / BasicStatistics,在 Basic Statistics 按下 View Statistics,觀察 Mean。
-
將 Square 接至 Hypothesis Test,設定 TestType = z_Test,Sigma = 0.03,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 大於預設值,虛無假設無法被拒絕,所以只能相信虛無假設,儀器並無偏差產生。
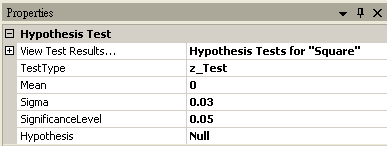
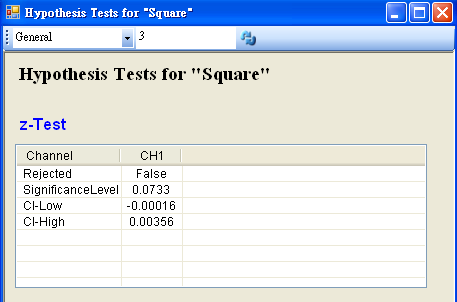
-
若再設定 Hypothesis Test 中 SignificanceLevel 為 0.1,將拒絕虛無假設的範圍加大,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 小於設定值,虛無假設被拒絕,所以否定虛無假設,故儀器有偏差產生,需重新加以校正。
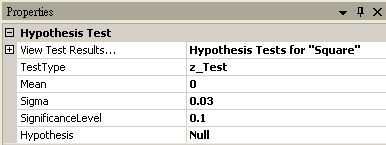
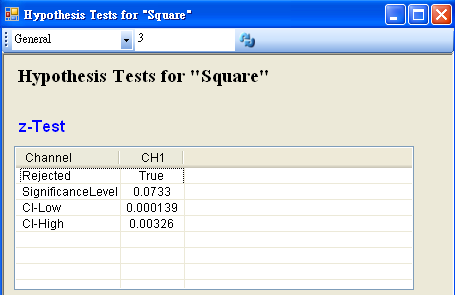
-
假設一個班級有 51 人,因為班上導師請假,想了解班上總成績是否因故下滑,而全校成績平均 55 分,假設虛無假設為班上成績並無因為老師請假而下滑,進行 t-Test。
-
首先以 Source / Noise 產生一組學生的成績,SamplingFreq 設定為 50,Amplitude 為 30,AmplitudeOffset 為 50,再連接至 Compute / Statistics / Basic Statistics,在Basic Statistics 按下 View Statistics,觀察 Mean。

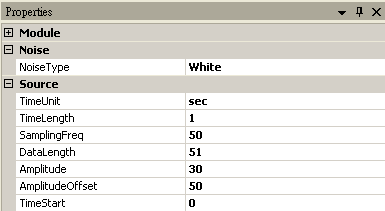
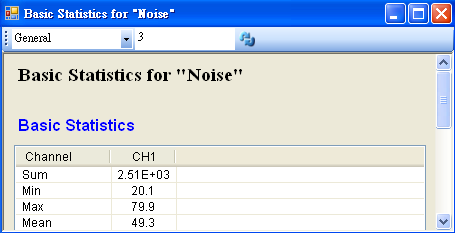
-
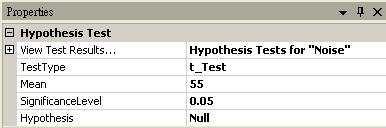
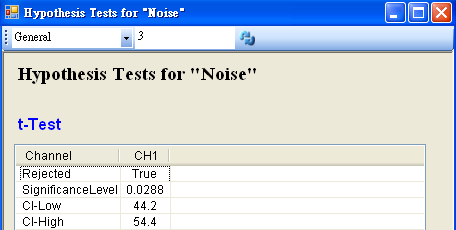
將 Noise 接至 HypothesisTest,設定 TestType = t_Test,Mean = 55,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 小於預設值,虛無假設被拒絕,所以因為老師請假而導致班上成績下滑。
-
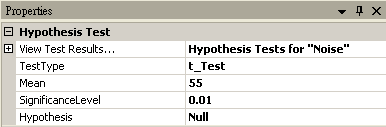
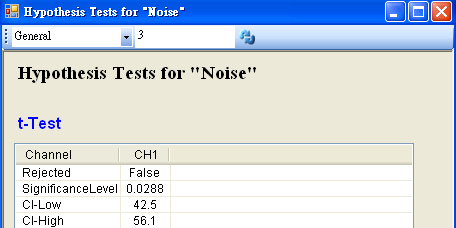
若再設定 Hypothesis Test 中 SignificanceLevle 為 0.01,將拒絕虛無假設的範圍變小,然後再以 View Test Results,觀察其檢定的結果,資料計算出的SignificanceLevel 大於設定值,虛無假設無法被拒絕,所以相信虛無假設,並不因為老師請假而造成成績下滑。
-
假設某銀行有五個窗口進行處理,客戶等待時間變異數為 10 分鐘,如今改成單一窗口處理,針對 101 位客戶進行調查,檢驗是否因為改成單一窗口之後,因此等待時間變異數變小,虛無假設為並無因為改變成單一窗口而使等待時間變異數變小,進行 Var-Test。
-
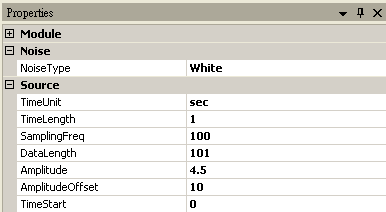
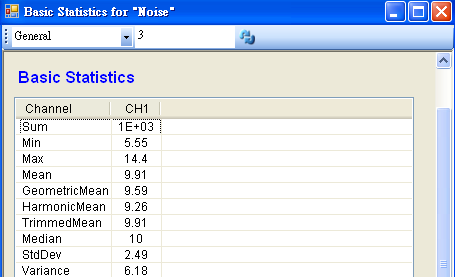
首先以 Source / Noise 產生 101 位客戶等待的時間資料,SamplingFreq 設定為 100,Amplitude 為 4.5,AmplitudeOffset 為10,再連接至 Compute / Statistics / Basic Statistics,在 BasicStatistics 按下 View Statistics,觀察 Variance。
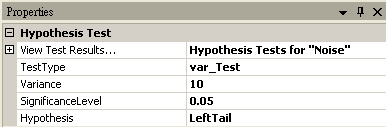
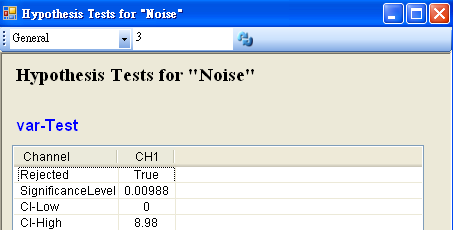
-
將 Noise 接至 HypothesisTest,設定 TestType = var_Test,Variance = 10,因為資料的變異數小於預設變異數,所以設定 Hypothsis = LeftTail,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 小於預設值,虛無假設被拒絕,因此推斷單一窗口等待時間的變異數變小。
相關指令
Noise、Square、Basic Statistics