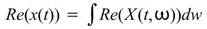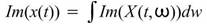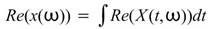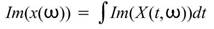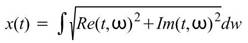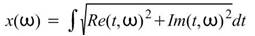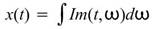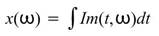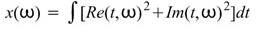本模組群提供時頻分析之計算:
-
Short Term Fourier Transform:短時傅立葉轉換。
-
Morlet Transform:小波轉換,此處之母函數為Morlet function。
-
Enhanced Morlet Transform (*Only in Professional):改良過的Morlet轉換,融合了Morlet與短時傅立葉之特性。
-
Hilbert Spectrum:將輸入訊號經Hilbert Transform後,計算出每個時間點的瞬時頻率。
-
Marginal Frequency / Marginal Time:將計算出之時頻分析結果對頻率域/時域作積分計算。
-
Transpose Spectra:將時頻圖的時間軸與頻率軸對換。
傅立葉轉換(FourierTransform)是將時間訊號轉換至頻率域。相較於傅立葉轉換,僅能呈現訊號振幅與相位隨頻率變化,但無法知道該頻率發生的時間點。 而短時傅立葉轉換 ( Short-Term Fourier Transform, STFT, or spectrogram ) 用以計算訊號強度與相位隨時間與頻率的分佈,解決傅立葉轉換(Fourier Transform)無法得知頻率發生的時間的缺點。
說明
數學式為
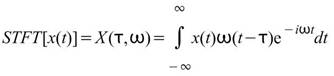
其中,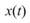 是輸入訊號,
是輸入訊號, 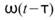 是一個窗函數。數學式中的意義為:每一時間點
是一個窗函數。數學式中的意義為:每一時間點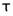 對
對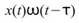 作傅立葉轉換,再將窗函數沿著時間軸方向挪移並計算得到的結果即為
作傅立葉轉換,再將窗函數沿著時間軸方向挪移並計算得到的結果即為
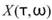 代表了訊號某一時間與頻率上的強度或相位。各窗函數的定義,請參閱
Fourier transform。
代表了訊號某一時間與頻率上的強度或相位。各窗函數的定義,請參閱
Fourier transform。
Windows size 與 Frequency resolution 之間的關係如下:
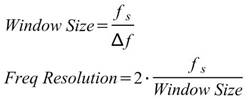
其中,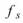 ,Frequency Resolution
設定的越低,計算窗函數會越長,訊號周期性越強,所以頻率越確定,時間不確定。Frequency
Resolution設定的越高,計算訊號的窗函數越短,時間越確定,頻率不確定
,Frequency Resolution
設定的越低,計算窗函數會越長,訊號周期性越強,所以頻率越確定,時間不確定。Frequency
Resolution設定的越高,計算訊號的窗函數越短,時間越確定,頻率不確定
參數設定(Properties)
本模組接受實數(real number),單通道(single channel),rgular的訊號(signal)、聲音訊號(audio)輸入;輸出訊號格式為複數,單通道的時頻(spectra)資料結構。各參數定義詳如下方圖表。
|
參數名稱 |
參數定義 |
預設值 |
|
FreqAxis |
時頻圖頻率的分佈可以設定為是 LinearAxis (線性尺度)或是 LogAxis ( 對數尺度),LogAxis 多用於聲音訊號分析。 |
LinearAxis |
|
FreqMin; FreqMax |
透過設定此參數,可決定繪圖時頻率的上下邊界。 |
0;0.5 * (Sample Frequency) |
|
FreqResolution |
此值會影響到窗函數的大小,設定的越低,窗函數會越長。 |
(Sample Frequency) / 40 |
|
FreqCount |
設定 STFT 於頻率方向之格點數。 |
256 |
|
TimeCount |
設定 STFT 於時間方向之格點數。 |
2048 |
|
RemoveDC |
此值決定在進行 STFT 分析前,要不要先移除直流訊號。 |
True |
|
Window |
在STFT 分析,進行時間軸的分割時,會利用窗函數進行濾波,此處可選擇不同窗函數。關於各窗函數的定義,請參閱 Fourier transform。 |
Gauss |
範例(Example)
以下範例以一個鳥鳴訊號 (Chirp ) 作輸入,利用 Visual Signal 作時頻分析,可以出現頻率隨時間線性變化。
-
按下 Network 工具列的
 ,或以 Source / Open
data from file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic)。
,或以 Source / Open
data from file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic)。
-
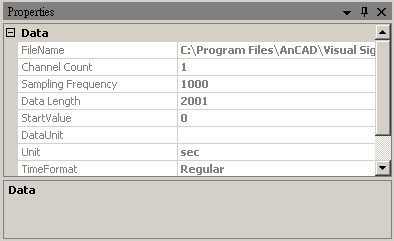
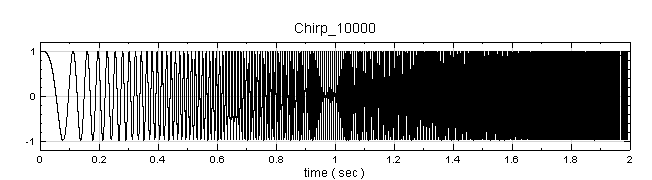
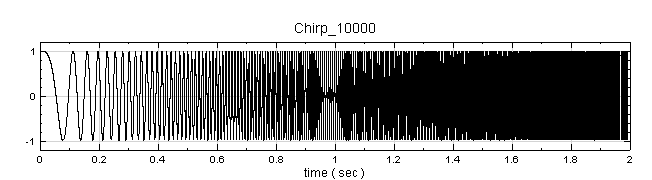
點選 Chirp_1000 圖示,其 Properties 下顯示此訊號的通道數 (Channel Count) 為 1,取樣頻率 (Sampling Frequency) 為 1000 Hz,再用 Viewer / Channel Viewer 繪製訊號。可觀察此訊號頻率隨時間漸增。
-
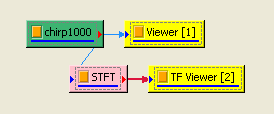
選擇 Compute / TFA / Short Term Fourier Transform 直接對此訊號作 STFT,以 Viewer / Time Frequency Viewer 繪出計算結果。觀察時頻圖,訊號頻率隨時間呈一直線的變化,且由結果可得到某個時間點訊號的頻率值。
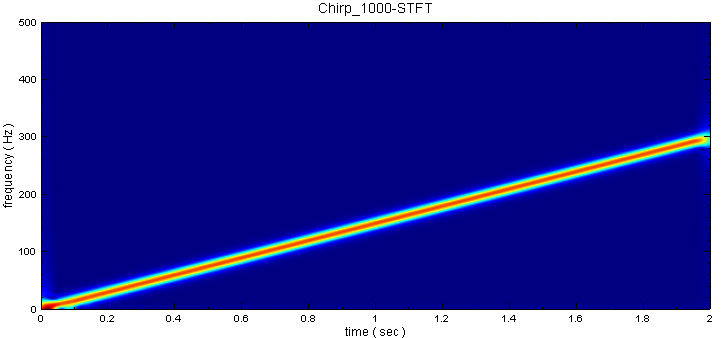
-
若是改變STFT 的參數 TimeCoant 或FreqCount,則STFT 會根據新設定的網格數量重新計算,因此會影響計算結果的解析度以及運算時間。現在改變 TimeCount 為 50,則運算速度變快,但結果的解析度亦變差。
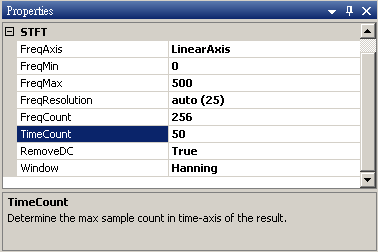
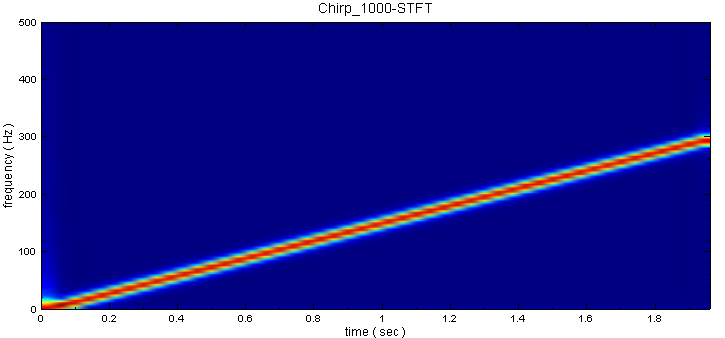
-
若是改變 FreqMin 或 FreqMax 參數,STFT 仍然會對原頻率範圍作計算,不過僅截取參數設定範圍內的資料作輸出,不會影響作 STFT 的計算量。改變 FreqMax 為 50,計算時間並未因此縮短。

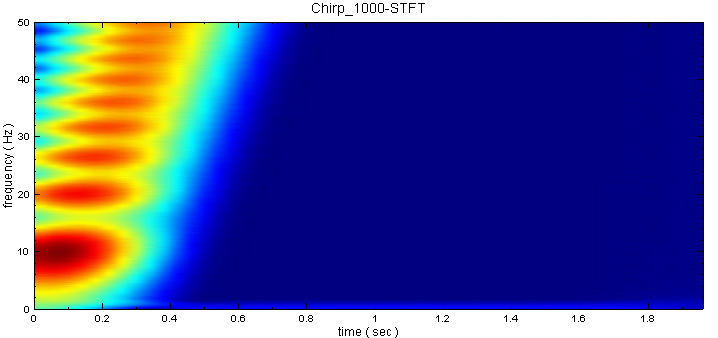
相關指令
Fourier Transform,Morlet Transform,Enhanced Morlet Transform。
參考資料
Stepphane Mallat, a Wavelet Tour of Signal Processing (2nd Ed), 1999.
小波分析 (Wavelet Analysis),或小波轉換 (Wavelet Transform) 是指用有限長或快速衰減的、稱為母小波 (Mother Wavelet) 的振盪波形來表示訊號。該波形被縮放和平移以匹配輸入的訊號。Morlet transform 即運用母小波 Morlet wavelet,對訊號進行小波分析的方法。
說明
與傅立葉轉換最大的不同,小波轉換將訊號轉為時間–頻率的訊號,根據測不準原理,頻率以及時間解析度的乘積為固定值,即是頻率解析度佳,則時間解析度一定差,反之亦然。短時傅立葉轉換的高低頻率帶的時間與頻率頻解析度皆為定值,但是在處理上,會希望在高頻帶的時間解析度佳,在低頻帶的頻率解析度較佳,唯有小波轉換,才能達到這樣的處理結果。小波轉換的方程式如下:
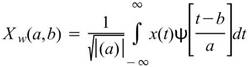
其中,a 參數為母小波縮放參數,b 為平移參數。再藉由轉換,將 a 值轉換為頻率。母小波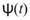 必須符合三個條件
必須符合三個條件
-
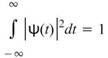 ,
, -
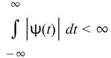 ,
, -
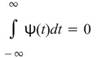
而 Morlet Transform 屬於小波轉換,其母小波的定義為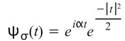 ,在 Visual Signal 中
,在 Visual Signal 中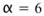 。
。
參數設定(Ploperties)
本模組接受實數(real number),單通道(single channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出訊號格式為實數,單通道,regular的時頻(spectra)資料。參數須設定起始與終點位置,其單位等於輸入訊號的時間單位。
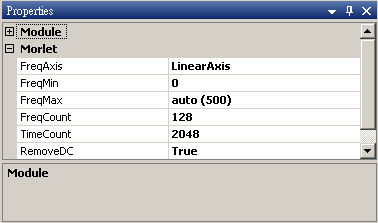
|
參數名稱 |
參數定義 |
預設值 |
|
FreqAxis |
時頻圖頻率的分佈可以設定為是線性尺度,或是 Log 尺度。Log 尺度提供聲音分析使用。 |
LinearAxis |
|
FreqMin; FreqMax |
透過設定此參數,可決定繪圖時頻率的上下邊界。 |
0; 0.5 * (Sample Frequency) |
|
FreqCount |
設定頻率方向之離散網格數。 |
128 |
|
TimeCount |
設定時間方向之離散網格數。 |
2048 |
|
RemoveDC |
此值決定在進行 Morlet Transform 分析前,是否先移除直流訊號。 |
True |
範例(Example)
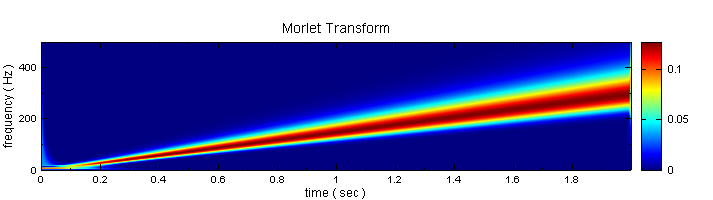
以下範例為一個鳥鳴訊號 (Chirp),利用 Visual Signal 分析其時頻圖,可以發現一個頻率隨時間線性變化。
-
按下 Network 工具列的
 ,或以 Source / Open
datafrom file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo\ Basic ),以 Viewer /
Channel Viewer 繪出。
,或以 Source / Open
datafrom file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo\ Basic ),以 Viewer /
Channel Viewer 繪出。
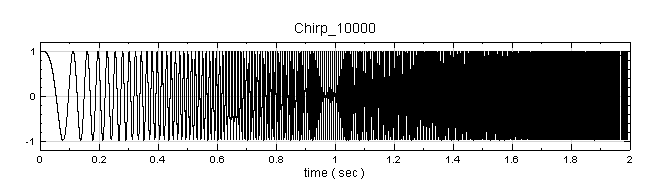
-
以 Compute / TFA / Morlet Transform 對輸入訊號作計算,再以 TFA Viewer 繪出,可明顯看到在越高頻的地方,頻率散佈範圍越大,轉換的效果越差。
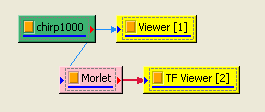
相關指令
Short Term Fourier Transform,Enhanced Morlet Transform。
參考資料
1.Stepphane Mallat, a Wavelet Tour of Signal Processing (2nd Ed), 1999..
2. Y.-N.Jeng, C.-T. Chen and Y.-C. Cheng, ”The Enhanced Morlet Transform via Iterative Filter to Study Turbulent Data Strings”, The 6th Aslan Computational Fluid Dynamics Conference Taiwan, August, 2005.
*Only in Professional*
Morlet Transform 的缺點是在高頻部分,由於頻率解析度下降的關係,所以高頻會發散,請查閱Morlet Transform 章節。Enhanced Morlet transform 預先以 Gauss 函數處理,以解決高頻處能量發散的狀況。
說明
在小波轉換之前,會先乘上一個高斯函數,拿掉較邊緣、低震幅的訊號,使高頻解析度增加。此轉換的方程式如下,見 Morlet 章節:
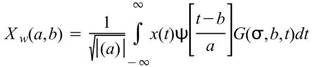
其中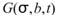 為高斯函數:
為高斯函數: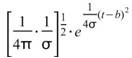
由於高頻部分,Morlet 小波的 Scale 參數 a 會減小,導致高頻的解析度會變差,於是在進行小波轉換之前,會先對
Morlet Wavelet 乘上一個 Gaussian Window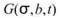 使得頻率解析度增加。
使得頻率解析度增加。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出訊號格式為實數,單通道,Regul(r的時頻(spectra)資料。各參數定義詳如下表。
|
參數名稱 |
參數定義 |
預設值 |
|
FreqAxis |
時頻圖頻率的分佈可以設定為是線性尺度,或是 Log 尺度。 |
LinearAxis |
|
FreqMin; FreqMax |
透過設定此參數,可決定繪圖時頻率的上下邊界。 |
0; 0.5 * (Sample Frequency) |
|
OverlappedFactor |
Gaussian window 移動時之重疊量,即為原式的 |
1 |
|
FreqCount |
設定頻率方向之離散網格數。 |
128 |
|
TimeCount |
設定時間方向之離散網格數。 |
2048 |
|
RemoveDC |
此值決定在進行 Morlet Transform 分析前,是否先移除直流訊號。 |
True |
範例(Example)
以下範例為一個鳥鳴訊號 (Chirp),利用Visual Signal 分析其時頻圖,可以發現頻率隨時間線性變化。
-
按下Network工具列的
 ,或以 Source / Open
data from file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic ),以 Viewer /
Channel Viewer 繪出。
,或以 Source / Open
data from file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic ),以 Viewer /
Channel Viewer 繪出。
-
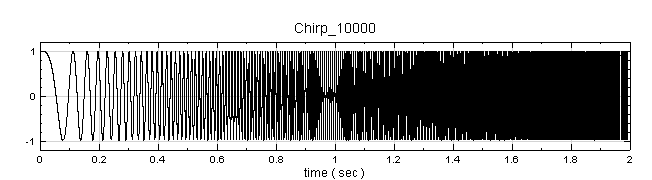
以 Compute / TFA / Enhanced Morlet Transform 對訊號作轉換, 以 TFA Viewer 繪出,可明顯看到在高頻段效果較 Morlet Transform 來的好。

相關指令
Short Term Fourier Transform,Morlet Transform。
參考資料
1.“觀察一維紊流數據的一種有效之新拆解法”, 鄭育能, 陳季聰, 鄭又齊, 第十二屆全國計算流體力學學術研討會。
2. A Wavelet Tour of Signal Processing (2nd Ed)
Hilbert Spectrum 利用 Hilbert Transform,計算訊號每個時間點的瞬時頻率與瞬時振幅,並輸出為 時間-頻率 的矩陣。在 HHT 過程中,EMD後將 IMF 由訊號中提取出來後,我們可順利的把Hilbert Transform 應用在各個 IMF 上,觀看 Hilbert Spectrum 得出之時頻分析結果。利用模組 Haar Transform 之輸出結果也可直接接上 Hilbert Spectrum。
說明
在此模組內,包含了兩種 Hilbert Transform 的方法,請參考 Hilbert Transform 元件中的敘述。
我們可對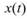 計算得到其 Hilbert
Transform
計算得到其 Hilbert
Transform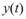 如下:
如下:
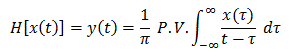
,其中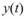 稱為
稱為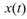 的Hilbert
pair。上式相當於
的Hilbert
pair。上式相當於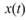 和
和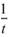 的
convolution後,再除以
的
convolution後,再除以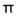 :
:
既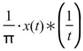 。( P.V. 為 Cauchy Principle
Value )
。( P.V. 為 Cauchy Principle
Value )
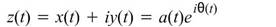
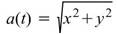
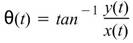
定義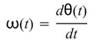 為瞬時角速度,而
為瞬時角速度,而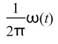 即為瞬時頻率。
即為瞬時頻率。
因此,Hilbert transform 後,可以得到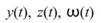 。
。
如欲畫為時頻圖,則依時間![]() 操作
操作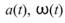 :
:
-
在時間為
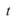 時,有頻率
時,有頻率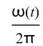
 可得在 Y軸上之高度
可得在 Y軸上之高度 -
在時間為
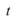 時,有強度
時,有強度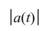
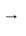 可得在 Z 軸上之大小
可得在 Z 軸上之大小
所有時間點操作,既可化為時頻圖,此為 Hilbert Transform 。而如此之操做實為將不連續的點畫在圖上,故多會插入高斯函數柔化數值。
若把 multi-channel 全部做 Hilbert transform 後,原訊號可表示成如下的形式(多用於 EMD 拆解後之下一步處理):
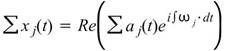
其餘操作同 single-channel。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出訊號格式為實數,單通道,regular的時頻(spectra)資料。參數定義整理如下。
|
參數名稱 |
參數定義 |
預設值 |
| Method | 選擇 Hilbert Spectrum 計算的方法,"HilbertSpectrum"使用傳統的 Hilbert Transform;"byEnvelope"為逸奇科技自行開發之方法。 | HilbertSpectrum |
|
FreqMin |
顯示Hilbert Spectrum時設定的最小頻率。 |
0 |
|
FreqMax |
顯示Hilbert Spectrum 時設定的最大頻率。 |
0.5 * (Sample frequency) |
|
FreqCount |
設定Hilbert Spectrum於頻率之離散網格數。 |
256 |
|
TimeCount |
設定Hilbert Spectrum於時間之離散網格數。 |
1024 |
|
Inst. Freq. Method |
計算瞬時頻率的方法,有Simple法與Robust法,請參考微分Diff 元件。 |
Simple |
|
Smoothing |
因Hilbert Spectrum為離散之數值,Smoothing是利用Gaussian函數使其平滑。 |
True |
範例(Example)
-
按下Network 工具列的
 ,或以 Source / Open
data from file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic),以 Viewer /
Channel Viewer 繪出。
,或以 Source / Open
data from file 讀取訊號檔,檔案 chirp1000.tfa 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic),以 Viewer /
Channel Viewer 繪出。
-
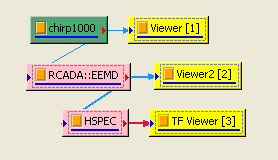
在 Chirp_1000後接上 Compute / HHT / RADAC EEMD計算出 IMF (Intrinsic mode function),再以 Viewer / Channel viewer 繪出。
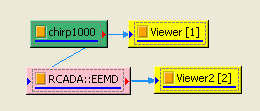
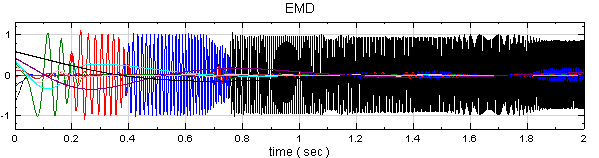
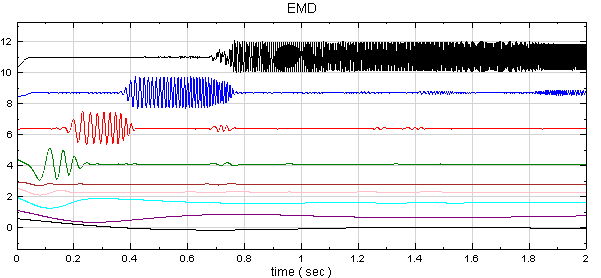
因 EMD 會計算出多通道訊號,用上圖表示不夠清楚,可以將 Channel viewer 的 Properties / ViewerHeight 調整為 300,Multi-channeldisplay 調為 List 使繪圖更清析可辨。
-
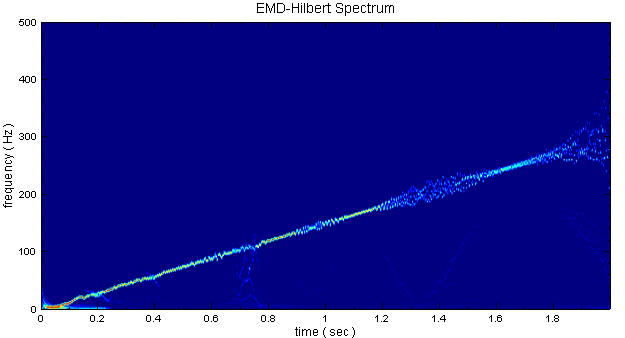
RADAC EEMD 後接上 Compute / TFA / Hilbert Spectrum,再以Viewer / Time-frequency viewer 繪出結果,此程序即為運用黃鍔法計算瞬時頻率。
-
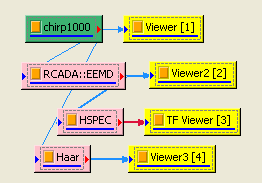
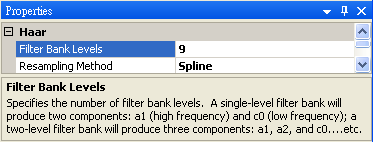
Hilbert Spectrum 也可由 Haar Wavelet Transform 計算瞬時頻率。在 Chirp_1000 後方接上 Compute / Transform / Haar Wavelet Transform,再把 Properties / FilterBank levels 調為 9,Resampling method選 Spline,最後仿照步驟 2~3 進行時頻計算。
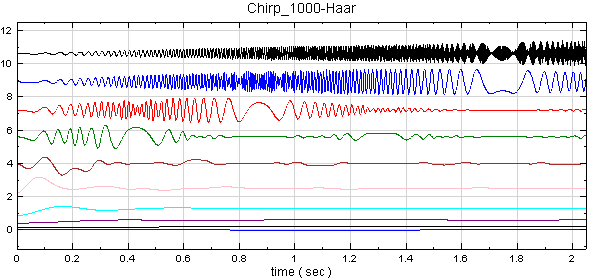
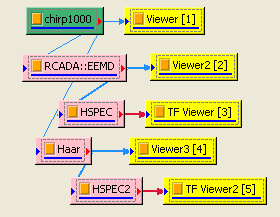
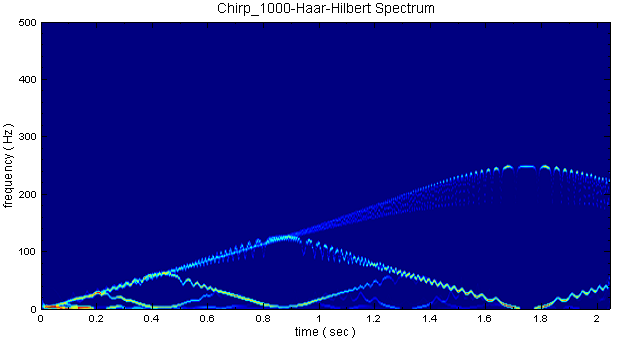
相關指令
RADAC EEMD,IMF Properties,TFA Viewer,Haar Transform。
參考資料
1. Proc. R. Soc. Land A 1998(903-995)
2. The Hilbert-huang Transform And Its Applications Huang, by Norden E. (EDT)/Shen, Samuel S. (EDT) World Scientific Pub Co Inc
利用時頻分析將一時域訊號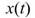 轉為時頻二維陣列
轉為時頻二維陣列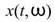 之後,提供使用者對 頻率軸 / 時間軸積分 後的 時間域 /
頻率域分佈。
之後,提供使用者對 頻率軸 / 時間軸積分 後的 時間域 /
頻率域分佈。
說明
在已處理過時頻分析的訊號,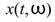 ,針對頻率軸積分,得到以時間為參數的分佈。數學上,這樣的操作可寫為:
,針對頻率軸積分,得到以時間為參數的分佈。數學上,這樣的操作可寫為:
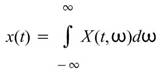
其中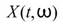 為時頻二維陣列,
為時頻二維陣列,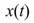 為時間域分佈,此即為 Marginal
Time。若針對時間軸積分,得到以頻率為參數的分佈。這樣的操作可寫為:
為時間域分佈,此即為 Marginal
Time。若針對時間軸積分,得到以頻率為參數的分佈。這樣的操作可寫為:
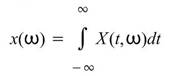
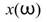 為頻率域分佈,此即為 Marginal
Frequency,而若此
為頻率域分佈,此即為 Marginal
Frequency,而若此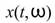 是由
是由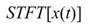 處理而得者,
處理而得者,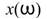 將與做傅立葉轉換無異。
將與做傅立葉轉換無異。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel),regular的時頻(spectra)資料輸入;輸出訊號格式為實數,單通道,regular的訊號(signal)。
參數為 Marginal Method,主要針對時頻二維複數陣列處理,與 時間軸 / 頻率軸 積分上採取不同的方法,內建5種選項,內容整理如下圖表。
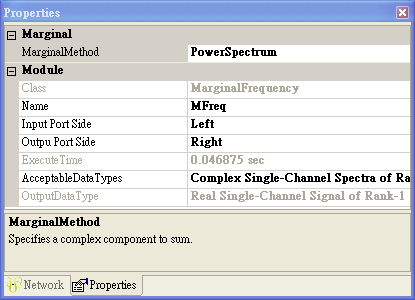
|
選項名稱 |
選項定義 |
|
Complex |
分別對實、虛部積分。
|
|
Magnitude |
對時頻訊號取 Norm 後再積分。
|
|
RealPart |
對時頻訊號實部積分。
|
|
ImagPart |
對時頻訊號虛部積分。
|
|
PowerSpectrum |
對時頻訊號取 Norm2後再積分。
|
範例(Example)
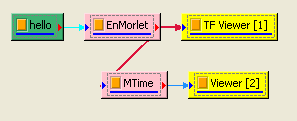
範例以聲音訊號 hello.wav 作為訊號源,利用 Visual Signal 中的 Enhanced Morlet Transform 分析其時頻圖,再以 Marginal Time 計算訊號時間域的分佈。
-
按下 Network 工具列的
 ,或以 Source / Open
data from file 讀取訊號檔,檔案 hello.wav 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic),接著做 Compute /
TFA / Enhanced Morlet Transfoam,再以 Viewer / Time Frequency Viewer
繪出結果。
,或以 Source / Open
data from file 讀取訊號檔,檔案 hello.wav 位在安裝目錄下data資料夾 ( 預設為 C : \
Program Files \ AnCad \ Visual Signal \ demo \ Basic),接著做 Compute /
TFA / Enhanced Morlet Transfoam,再以 Viewer / Time Frequency Viewer
繪出結果。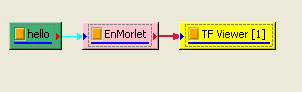
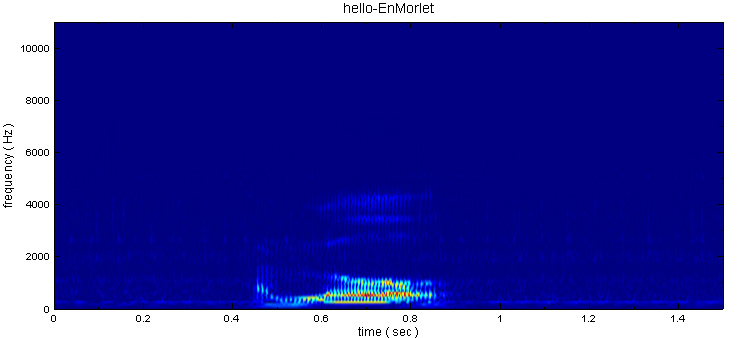
-
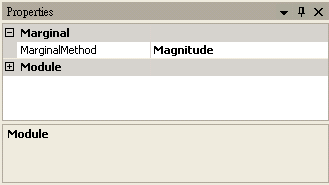
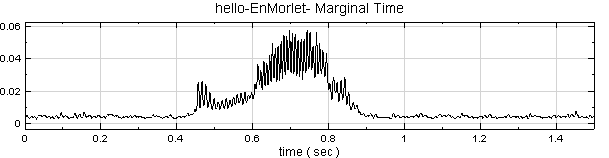
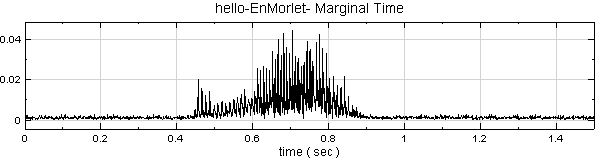
於 EnMorlet 後面作 Compute / TFA / Marginal Time,MarginalMethod 設定為 Magnitude 計算,以ChannelViewer 繪出,圖中縱軸為振幅。
-
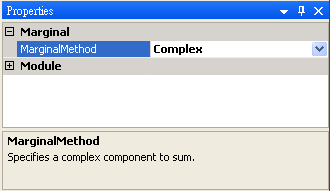
將 MarginalMethod 調整為 Complex,代表 Marginal Time 直接對時頻訊號作積分。
-
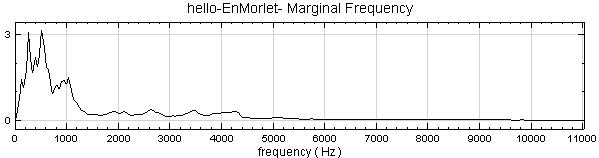
再於 EnMorlet 後面作 Compute / TFA / Marginal Frequency,其計算結果之橫軸為頻率,縱軸為振幅。
相關指令
STFT,Morlet Transform,Enhanced Morlet Transform,Marginal Frequency。
將時頻圖或階次圈數圖(Spectra)進行轉置,將資料的 X 軸和 Y 軸對調。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel),regular的時頻(spectra)資料輸入
範例(Example)
以下範例為 OrderSpectrogram by STFT 的計算結果再經過轉置的結果,流程如如下圖。
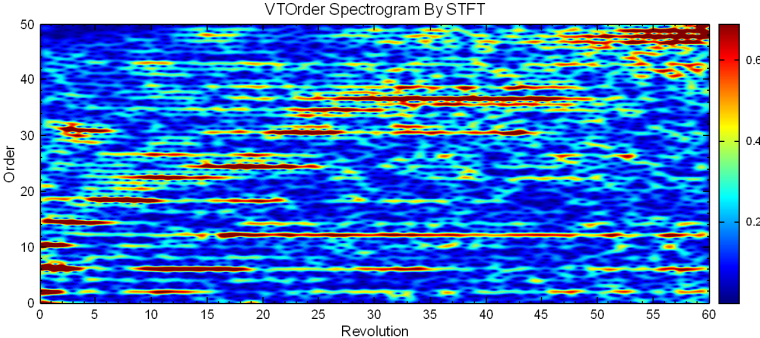
將 OrderSpectrogram by STFT 結果接至 Transpose Spectra 轉換之後,最後利用 TF Viewer 觀看其結果。
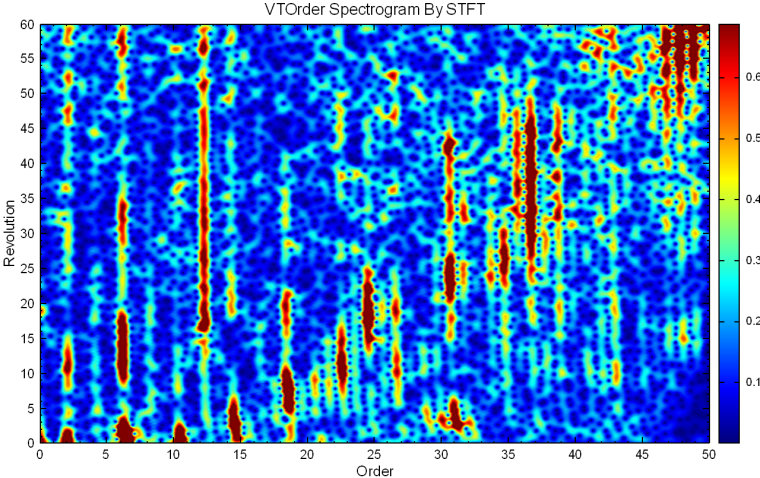
相關指令
OrderSpectrogram by STFT、OrderSpectrogram by EnMorlet、STFT。