Hilbert-HuangTransform ( HHT ) 是一種根據經驗而來的訊號處理方式,利用這個方式可由非穩態 ( Unsteady ) 及非線性 ( Non-linear ) 的訊號中提取有物理意義的資訊。一般傳統的訊號處理方式多半建立於線性和穩態的假設上,一直到近年才發展出一些數學方法處理非穩態或非線性的訊號,但現實生活中很多情況是需要處理同時具有非穩態和非線性的訊號,這正是做訊號處理時令人頭痛的難題,然而由黃鍔博士所發展的一套數學方法─ Hilbert-Huang Transform ( HHT ) 即針對上述情況提供一種解決方案。HHT 計算包含兩個部份:EMD ( Empirical Mode Decomposition ) 和 Hilbert Spectrum,結合 EMD 與 Hilbert Transform 讓此方法具有處理非穩態且非線性訊號的潛力,特別是需要同時知道時間、頻率、能量的變化關係時。在多數研究中,HHT 可得到更豐富的時間、頻率、能量的關係,且在很多情形下,我們可藉由 HHT 提取出更有物理意義的資訊,從而解釋物理現像,並解決工程問題。
-
RCADA EEMD:中央大學數據中心所提供的一種 EEMD 演算法。
-
IMFProperty:列出各 IMF 的過零點個數、極值個數、過零點個數的平均頻率、各 IMF 間的正交性、各 IMF 具有的功率比例。
-
AnCAD EMD (*Only in Professional): 逸奇科技所提供的各種不同的 EMD 拆解演算法,提供使用者更多選擇。
RCADA EEMD 為中央大學數據中心的最新 ( 2009 ) EEMD 演算法,此模組的預設條件與數據中心提供 MATLAB 原始碼的 EEMD 函式相同,但本模組更提供多種邊界條件、亂數產生方式等參數選擇,以供使用者選擇,並且運算速度較原本數據中心提供 MATLAB 原始碼增加 200 倍以上。
說明
詳請參考http://rcada.ncu.edu.tw/research1.htm。
參數設定(Properties)
本模組接受實數(real number)訊號。RCADA EEMD 僅接受單通道(single channel), regular 的訊號(signal)或聲音訊號(audio)輸入。

|
參數名稱 |
參數定義 |
預設值 |
|
SplineType |
提供三種邊界條件 ( Boundary Conditions ),包括 Clamped Spline、Nature Cubic Spline、Not A Knot。下面表格將說明。 |
NotAKnot |
|
Number of Ensembles |
運行 EEMD 時,添加 Noise 的次數,並且會計算出多少組的 IMF 結果再進行平均。例如預設為 20,將原訊號加入 20 次的 Noise ,並個別計算出20組 IMF 結果,並平均之。 |
20 |
|
Noise Level |
即在運行 EEMD 時,添加的 Noise 之振盪,相對於原本訊號標準差之比值。 |
0.1 |
|
Max. Sifting Iterations |
進行 EEMD 求解時,疊代次數的上限。 |
10 |
|
Number of IMFs |
拆解出來的 IMF 通道總數。 |
-1 |
|
Modify Envelope Endpoints |
設定包絡線端點是否要進行外插計算。 |
True |
|
Use Guassian Noise |
設定是否使用 Guassian Noise,否則將使用 White Noise。 |
Fasle |
|
邊界條件 |
定義 |
|
NotAKnot |
邊界 ( 最鄰近) 上的點,其三次導數相等。此預設邊界條件等同於中央大學數據中心的 MATLAB 原始碼的 EEMD,但由於 Visual Signal 與 MATLAB的亂數產生不相同,拆解結果會稍有不同。 |
|
NatureCubicSpline |
邊界上的點,其二次導數為零。 |
|
ClampedSpline |
邊界上的點,其一次導數為定值 ( =0 )。 |
範例(Example)
-
本範例是採用中央大學網站上提供的範例資料 ( gsta.dat )。為一年一筆之地球表面平均溫度之資料,可以參考 C: \ Program Files \ AnCAD \ Visual Signal \ demo \ HHT 中的 demo68。
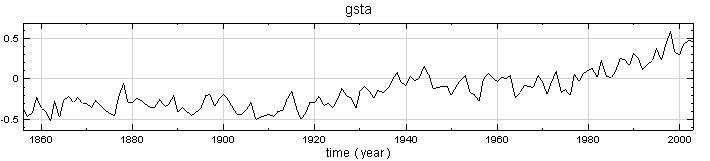
-
再將原訊號連接 Compute / HHT / RCADA EEMD 做拆解,參數設定為預設,其結果如下,注意到 Residual (即最後一條訊號,淡藍色線條),代表溫度的趨勢:
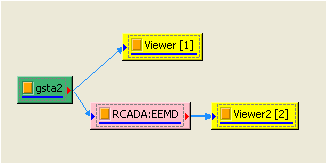
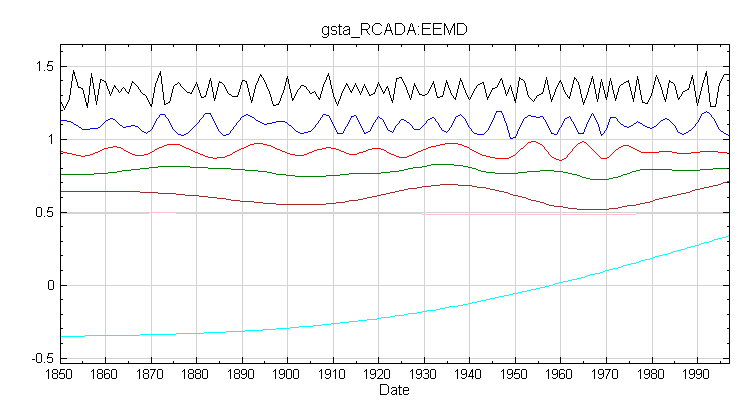
-
再對相同的訊號,比較 RCADA 提供 MATLAB 原始碼在 MATLAB 程式 與 Visual Signal的速度,
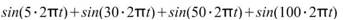 ,訊號長度為 20000,RCADA EEMD
拆解後結果如下:
,訊號長度為 20000,RCADA EEMD
拆解後結果如下:
在 Intel Dual Core E6300 (2.8GHz) 的電腦上,Visual Singal 的所花費計算時間為 1.65 秒,MATLAB為376.60 秒, 速度相差超過 200 倍。
-
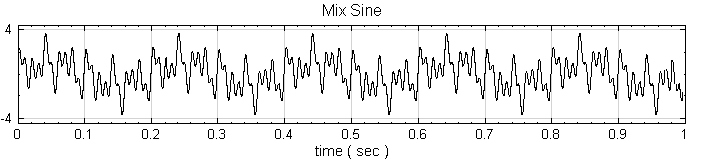
先參考 C: \ Program Files \ AnCAD \ Visual Signal \ demo \ HHT 中的 demo68_1,裡面資料 ( Wave ) 為錄製一段 Hello 的聲音,如下兩張圖。
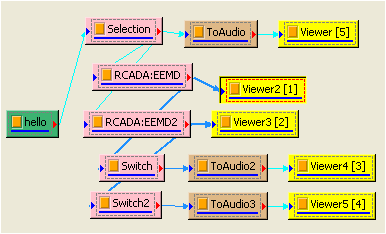
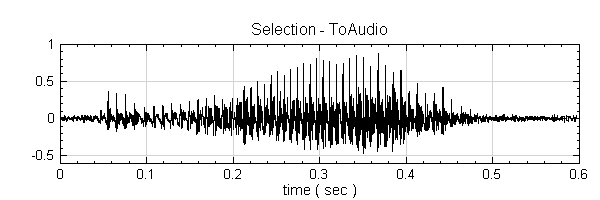
-
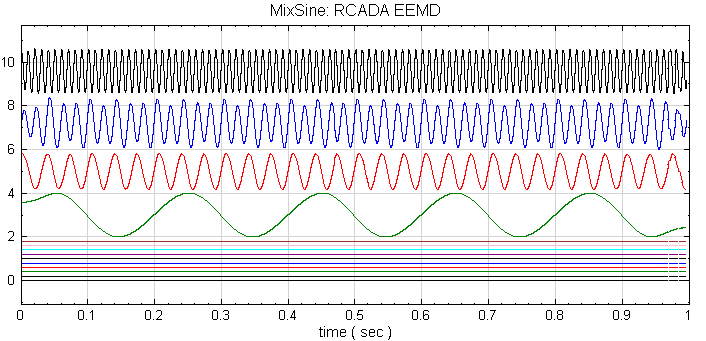
在 RCADA : EEMD 的參數中,Number of Ensembles 為 200,Noise Level 為 0.25,並觀察第三個通道的訊號,結果如下圖。。
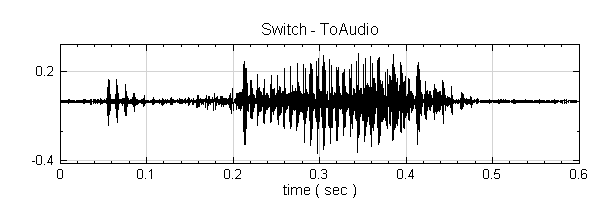
-
在 RCADA : EEMD2 的參數中,Number of Ensembles 為 1,Noise Level 為 0.1,並觀察第三個通道的訊號,結果如下圖。。
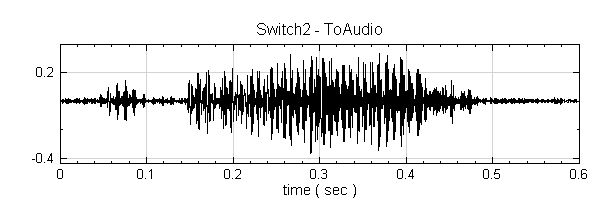
兩個拆解出來的訊號聽起來,發現第一個 EEMD 拆解出來的聲音比較清楚,第二個 EEMD 的結果含有一些噪音干擾。
相關指令
RCADAInstant frequency , RCADA Spectrum , AnCAD EMD
參考資料
1.http://rcada.ncu.edu.tw/research1_clip_reference.htm
2. Norden E. Huang, Zheng Shen, Steven R. Long, Manli C. Wu, Hsing H. Shih, Quanan Zheng, Nai-Chyuan Yen, Chi Chao Tung and Henry H.Liu :"The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis" , Proceedings of the Royal Society , Vol.454, No.1971, 1998
3. Huang, N. E., M. L. Wu, S. R. Long, S. S. Shen, W. D. Qu, P. Gloersen, and K. L. Fan (2003): "A confidence limit for the Empirical Mode Decomposition and Hilbert Spectral Analysis", Proc. Roy. Soc. London, 459A, 2317-2345.
4. ZhaoHua Wu and Norden E. Huang, 2009, " Ensemble Empirical Mode Decomposition : A Noise-Assisted Data Analysis Method " , Advances in Adaptive Data Analysis, Vol. 1, No. 1 (2009) 1–41
訊號經過各種 EMD 運算後,可分解成數個 IMF 和一個 剩餘訊號,IMF property 的功能是觀察各 IMF 的特性,目的是了解各種 EMD 是否適當的將訊號分離。
說明
EMD 分解出的 IMF 有零點和極值之數量差小於一的特性,為驗證 EMD 分解訊號的能力,可由此元件觀察各 IMF 的特性。此元件列出各 IMF 的過零點個數、極值個數、過零點個數的平均頻率、各 IMF 間的正交性、各 IMF 具有的功率比例。
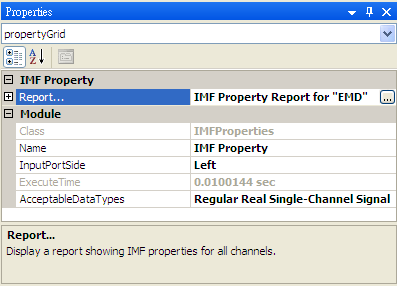
參數設定(Properties)
|
參數名稱 |
參數定義 |
|
General properties |
顯示個通道訊號的過零點次數(Zero Crossings)、局部最大(或最小)值的次數(Extreme Counts)、平均瞬時頻率、平均瞬時週期,與各通道能量比例 (Power)。其中平均瞬時頻率是以過零點次數與局部最大(或最小)值的次數來概略估計其訊號頻率,而各通道的能量為各個通道佔原訊號總能量(不算殘餘訊號 Residual)的百分比。 |
|
Orthogonality |
輸入訊號之各通道彼此之間的正交性矩陣。 |
範例(Example)
範例以 IMF Property 元件觀察 RCADA EEMD 運算分解後之訊號特性,點選 EMD 運算元件,按右鍵選擇 Compute / HHT / IMF Property,如下圖所示。分析的各個 IMF 特性可在屬性中,點選 Report… 屬性,其右方會出現一按鈕,點選按鈕可顯示此元件的分析結果,顯示的結果如下。

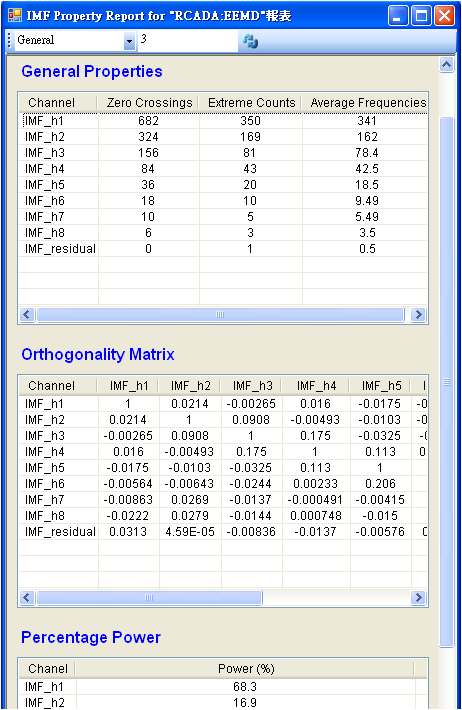
左上角第一個欄位是選擇顯示方法,可為一般(General)、科學記號(Scientific)以及固定小數點位數(Fixed);第二欄是決定位數,對一般決定總位數,而對固定小數點位數與科學記號是只決定小數點位數。第三個按鈕是決定前兩者後,更新顯示結果。
相關指令
EMD、Viewer。
*Only in Professional*
EMD 全名為 Empirical Mode Decomposition,是個依照訊號特性將訊號分解成數個 IMF ( Intrinsic Mode Functions ) 和一個剩餘訊號 ( Residual ) 的數學工具。較傅立葉級數分解更為優異的是,EMD分出的 IMF ,其振幅和瞬時頻率可以隨時間變化,並包留了原訊號中非線性和非穩態的特性。
說明
EMD 可依據訊號特性將原訊號分解為多個子訊號。相較於其他數學方法,EMD是一個適應性的運算方法,無論訊號為何,這個方法皆可以把訊號初步分解成較具意義的分量,但是要分得好就需要一點經驗與技巧了。這個訊號處理方法假設每一個訊號內部都包含不同的簡單震動模態,此震動模態稱為 Intrinsic Mode Function (IMF),理想的 IMF 均包含下面幾個特性:
-
零點和極值的數量相差在一個以下。
-
任一處的上包絡線(由局部極大值定義)和下包絡線(由局部極小值定義)的平均值為零(即對稱)。
Sifting 是做 EMD 計算時,從訊號中提取 IMF 的過程,依據上述對IMF的描述, Sifting 的運算流程如下:
-
取得一段要處理的訊號 x( t ),找出其局部極大值所在點,並以 Cubic Spline 方法將所有局部極大值相連,可得此訊號的上包絡線。
-
同樣的找出此訊號的局部極小值並以 Cubic Spline 方法相連,可得訊號的下包絡線。
-
計算上包絡線和下包絡線的平均值,可得一平均線,令此平均線為 m( t )。
-
將原訊號和平均線相減,令相減後所得的訊號為 h( t ),則 h( t ) = x( t ) - m( t )。
上述由 x( t ) 減去上下包絡線的平均線 m( t ),求得 h( t ) 的過程即為 Sifting。
本模組提供兩種 Sifting 疊代終止準則:
-
Cauchy 收斂測試,疊代過程中連續兩次 Sifting 後的訊號標準差
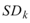 (參數StandardDeviation)小於一給定的數值,則終止後續的
Sifting 動作
(參數StandardDeviation)小於一給定的數值,則終止後續的
Sifting 動作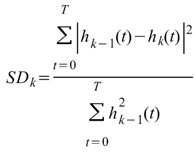
-
先選定一個篩選次數上限,將原訊號做 Sifting,直到新訊號過零點個數和極值個數之差小於 1 為止,但篩選次數不超過所選定的次數上限(參數Max. Sifting Iterations)。*注意此條件與論文中的不一樣,但是為避免篩選後的訊號無法收斂到終止條件,而做此設計。
1 與 2 兩種準則是同時比較,兩者只要滿足其一即達收斂標準,Sifting 動作就結束。Visual Signal 會將拆解出來的結果依高頻至低頻方式輸出 (Channel 1 頻率最高,Channel 2 次之,以此類推),殘餘訊號放在最後一條 Channel。
EMD 的運算如下:將一原始訊號做若干次 Sifting 後,訊號上、下包絡線的平均線會漸漸和水平軸重合,直至訊號的上、下包絡線對稱於水平軸。此新訊號即為第一個 IMF,故稱為 IMF1。將 IMF1 從原始訊號減去,得到第一個殘餘訊號( First Residual ),稱為 r1,將 r1 依同樣方式做若干次 Sifting,可獲得 IMF2,再將 IMF2 從 r1 扣除,得到第二個殘餘訊號 r2,依此規則重複計算,則可將原始訊號拆解成數個 IMF 和最後的殘餘訊號,此即為 EMD 的運算流程。
參數設定(properties)
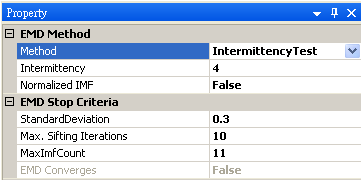
本模組接受實數 (real number)、單通道 (Single channel),regular 的訊號 (signal) 或聲音訊號 (audio) 輸入,其參數意義與設定如下:
|
參數名稱 |
參數定義 |
預設值 |
|
Method |
設定 EMD 運算時的方式,以下將介紹可設定的功能。 (1) Standard:以一般標準方式計算。 (2) IntermittencyTest:訊號中若有個極微幅的震動會產生一個局部極大值和及局部小值,利用此方法可適當忽略過於微小振動產生局部極值。 (3)EnsembleEMD:於輸入訊號上加一微小振幅的 white noise 後再作 EMD,此法無需預先設定參數,即可有效分離各尺度之 IMF。 |
IntermittencyTest |
|
Normalized IMF |
將所有 IMF 正規化。 |
False |
|
StandardDeviation |
設定門檻值,即公式中的 |
0.3 |
|
Max. Sifting Iterations |
Sifting 的最高次數。見說明疊代終止準則 2。 |
10 |
|
MaxImfCount |
決定每次 EMD 運算時,提取 IMF 的最大個數。 |
11 |
若是 Method 為 IntermittencyTest,必須有多一個參數 Intermittency 要設定,如下表。
|
參數名稱 |
參數定義 |
預設值 |
|
Intermittency |
兩極值間的最大的點數間距。超過的此範圍的極值會被忽略。此數值在每一模態中會自動增加成前一模態的兩倍。 |
4 |
若是 Method 為 EnsembleEMD,必須有多兩個參數要設定,如下表。
|
參數名稱 |
參數定義 |
預設值 |
|
Number of Ensembles |
運行 EEMD 時,添加 Noise 的次數,並且會計算出多少組的 IMF 結果再進行平均。例如預設為 20,將原訊號加入 20 次的 Noise ,並個別計算出 20 組 IMF 結果,並平均之。 |
20 |
|
Noise Level |
即在運行 EEMD 時,添加的 Noise 之振盪,相對於原本訊號標準差之比值。 |
0.1 |
範例(Example)
示範一混合訊號作 EMD 分析:
-
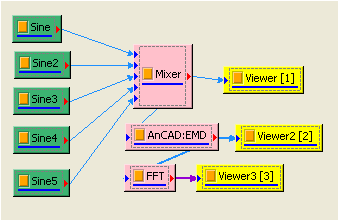
於 Project 視窗選擇 Source / Sine Wave 產生訊號,並設定其參數,時間長度為 1.5 秒,頻率為 20;並再設定一 Custom Wave 為 Exp ( 1.8 * t ),一樣時間長度為 1.5 秒。以 Comput / Math / Mixer 混合兩者:
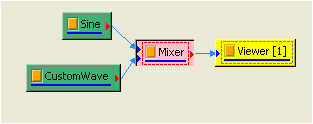
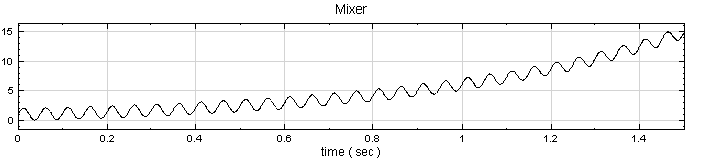
-
在Mixer後接上ComSute/HHT/EMD,再以Channel Viewer繪製計算結果,於Viewer的Properties/Channel/Multi-Channel Display選擇List,將每個IMF分開顯示,其圖示如下。
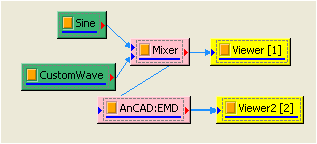
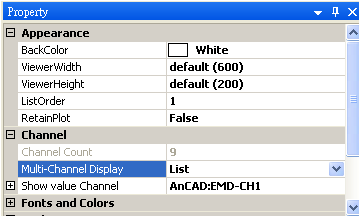
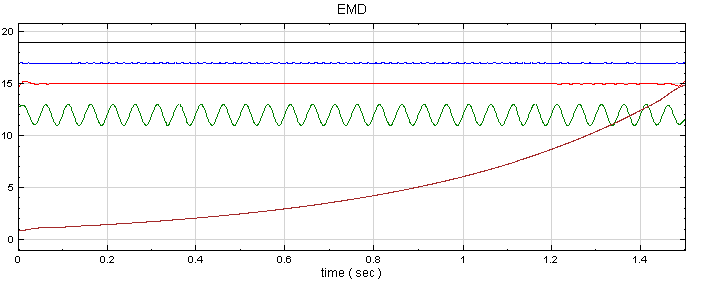
在此可發現原本的 Sin 函數與 Exponential 函數被徹底拆解,原本的 Sin 為 Channel 4,Exponential 函數則為殘餘訊號(因為Exponential 函數毫無週期性,無法再從中拆解出其他訊號)。其餘三筆訊號 ( Channel1 ~3 ) 是 EMD 在計算上過渡出來的結果,並無實質意義。
特別注意,EMD 具有自發性的依頻率拆解能力。若我們將不同頻率的 Sine Wave 混合,間隔 30Hz,由頻率 10Hz 至 130Hz,再以 EMD 處理後接上傅立葉轉換,可得下面結果:
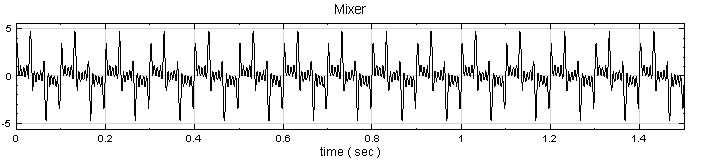
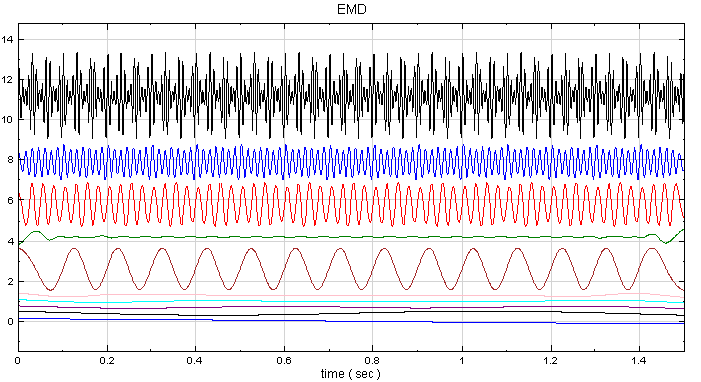
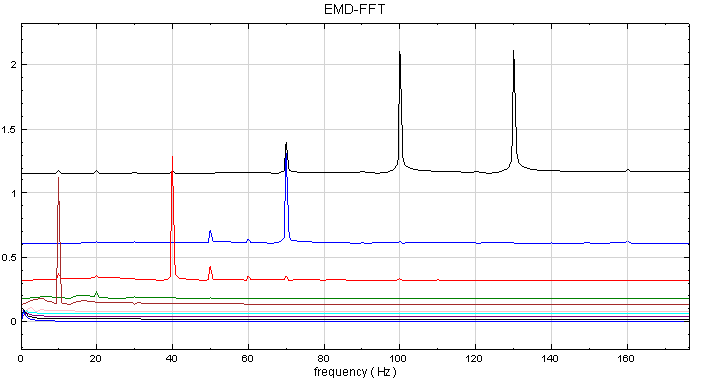
在此可發現 EMD 把訊號依頻率分離,但並沒有分的十分清楚。
EMD 使用上多結合 Hilbert transform 與 Hilbert Spectrum,做為HHT 標準程序。
EMD 輸出結果接上 Channel Switch ,選擇有興趣的通道後再連結上 Hilbert transform 可求得該通道之瞬時頻率;亦可將 EMD 輸出直接接上 Hilbert Spectrum,觀查 EMD拆解後的 HHT 時頻圖。
相關指令
Hilbert transform、IMF Properties、Hilbert Spectrum。
參考資料
Norden E. Huang, Samuel S.P. Shen, "Hilbert-Huang transform and its applications," London : World Scientific, c2005