*This module is available in Professional only*
*Only in Professional*
本模組用以處理 A、B 兩矩陣間的計算問題:
-
矩陣加法:
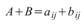 ,其中矩陣 A 與 B 的大小必須一致,皆為 M *
N。
,其中矩陣 A 與 B 的大小必須一致,皆為 M *
N。 -
矩陣減法:
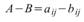 ,矩陣 A 與 B 的大小必須一致,皆為 M *
N。
,矩陣 A 與 B 的大小必須一致,皆為 M *
N。 -
矩陣乘法:
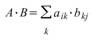 ,A 的大小為 M * N,B 的大小為 N *
P。
,A 的大小為 M * N,B 的大小為 N *
P。 -
矩陣左除法:
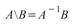 ,A 的大小為 M * N,B 的大小為 M *
P。
,A 的大小為 M * N,B 的大小為 M *
P。 -
矩陣右除法:
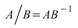 ,A 的大小為 M * N,B 的大小為P *
N。
,A 的大小為 M * N,B 的大小為P *
N。
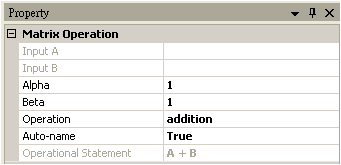
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出亦為同型態的資料。
|
參數名稱 |
參數定義 |
預設值 |
|
Input A |
A 矩陣的名字 |
僅輸出供使用者參考 |
|
Input B |
B 矩陣的名字 |
僅輸出供使用者參考 |
|
alpha |
A 的加權數 |
1 |
|
Beta |
B 的加權數 |
a |
|
Operation |
運算元,可為加,減,乘,左除與右除。 |
addition |
|
Auto-name |
若為 true,在 A+B 的情況下,模組的名為 A+B (隨運算元而不同改變);反之則為 Mop。 |
true |
|
By Element |
設為"True"時,運算模式為每個元素做運算,而非矩陣運算。 |
False |
|
Operation statement |
運算表示式 |
僅輸出供使用者參考 |
以加法為例:輸出的矩陣為 C,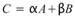 ,
,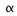 與
與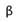 分別為 A、B 兩矩陣的權數。
分別為 A、B 兩矩陣的權數。
範例(Example)
-
以DoMatlab 模組產生一亂數 3 * 3的方陣:
矩陣內容如下:

以 Inverse Matrix 求解反矩陣,得到結果如下:

可把這結果與原本的矩陣相乘,確定相乘後的結果為單位矩陣。
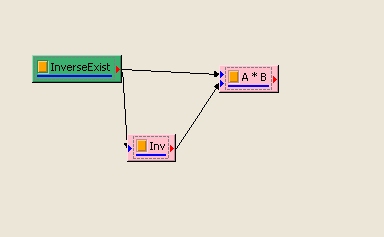
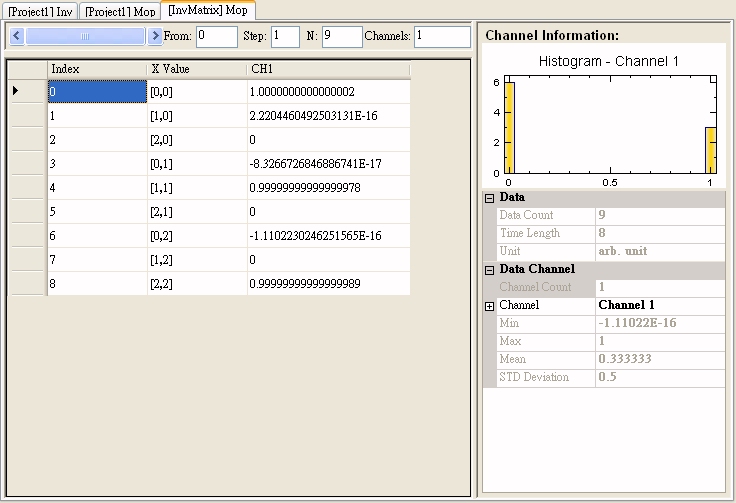
相關指令
Matrix Operation
參考
Gilbert Strang: Linear Algebra and Its Applications 3rd edition
*Only in Professional*
計算矩陣 A ( A 必須為方陣 ) 的反矩陣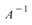 ,使
,使 ,I 為單位矩陣。
,I 為單位矩陣。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出亦為同型態的資料。
範例(Example)
-
以 DoMatlab 模組製造一亂數 3 *3 的方陣:
矩陣內容如下:

以 Inverse Matrix 求解反矩陣,得到結果如下:


可把這結果與原本的矩陣相乘,確定相乘後的結果為單位矩陣。
若輸入的矩陣為 Singular,好比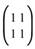 ,用此模組做計算,會發出 Warning :
,用此模組做計算,會發出 Warning :
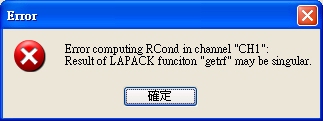
說明此矩陣為 Singular
相關指令
Matrix Operation
參考
Gilbert Strang: Linear Algebraand Its Applications 3rd edition
*Only in Professional*
將矩陣 A 做轉置,並可選擇是否做共軛。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出亦為同型態的資料。

|
參數名稱 |
參數定義 |
預設值 |
|
Complex Cojugate |
若矩陣為複數矩陣,是否要取共軛。 |
true |
範例(Example)
2 X 3 的 A 矩陣,矩陣內容如下:
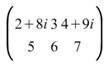
取轉置,但不取共軛,則輸出的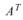 矩陣為
矩陣為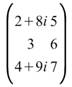
若同時取共軛,輸出的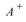 矩陣為
矩陣為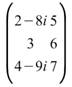
參考
Gilbert Strang: Linear Algebra and Its Applications 3rd edition
*Only in Professional*
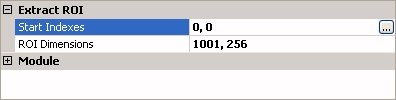
由矩陣 A 中截取矩陣 S。由 Start Indexes 為 [ sx , sy]開始截取一段長度為 lx ( Row )、ly ( Column ) 的矩陣。其 End Indexes 為 [ sx + lx - 1, sy + ly - 1],若 End Index 超過 A 的範圍則填零。
說明
非常類似矩陣定義中的 Sub-Matrix 定義,但此模組可用以處理更高維度的資料,此外超過原矩陣範圍者,本模組會填補上零。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出亦為同型態的資料。
|
參數名稱 |
參數定義 |
預設值 |
|
Start Indexes |
截取的起點座標。 |
( 0 , 0 ) |
|
ROI Dimensions |
截取的 Row 長度及 Column 長度。 |
原矩陣的 Row 長度及 Column 長度 |
範例(Example)
-
以 DoMatlab 模組製造一亂數 3 * 3 的方陣
矩陣內容如下

若截取的起點座標為 ( 0 , 0 ),ROI Dimensions 為 ( 3 , 1 ),截取到矩陣為
 。
。
若起點為 ( 2 , 2 ) ,ROI Dimensions 為 ( 3 , 3 ) ( 超過範圍 ),截取到矩陣為:
 ,超過範圍部份補零。
,超過範圍部份補零。
參考
Gilbert Strang: Linear Algebra and Its Applications 3rd edition
*Only in Professional*
將向量由矩陣 ( 或陣列,不見得必須為二維 ) 中提取出來。若提取的範圍超過原陣列大小,超出部份填補零。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出亦為同型態的資料。
|
參數名稱 |
參數定義 |
預設值 |
|
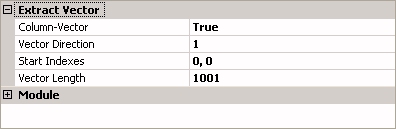
Vector Direction |
截取矩陣的方向,從零開始。好比有個四維陣列,若輸入的方向為 2,即是延著第三個維度的方向(通常稱為深度)截取。 |
0 (行方向) |
|
Column-Vector |
設定為 "True",輸出矩陣以一行 (Column) 為主依序排列,反之則相反。 |
True |
|
Start Indexes |
截取的起點座標 |
( 0 , 0 ) |
|
Vector Length |
截取的長度 |
原陣列在某各方向上的長度 |
範例(Example)
2 * 3 的 A 矩陣:
矩陣內容如下

設定 Column Vector 設為 True:截取方向為 0 (行方向),起點為 ( 0 , 0 ),長度為 3 (超過範圍)的向量。
所得到的結果為

參考
GilbertStrang: Linear Algebra and ItsApplications 3rd edition
*Only in Professional*
本模組用以截取矩陣(必須為方陣)的對角元素,並排列為一向量。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出亦為同型態的資料。

|
參數名稱 |
參數定義 |
預設值 |
|
Column-Vector |
設定為 "True",輸出矩陣以一行 (Column) 為主依序排列,反之則相反。 |
True |
範例(Example)
-
以DoMatlab 模組製造亂數 3 * 3 的方陣:
矩陣內容如下

截取得到的 Diagonal Vector 為

相關指令
Matrix Operation
參考
Gilbert Strang: Linear Algebra and Its Applications 3rd edition
*Only in Professional*
計算 1 / C。其中 C 為矩陣的 Condition Number。
說明
給定一個矩陣 A,A 的 Condition Number 定義為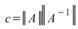 。C 可用
。C 可用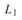 或
或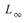 量測,分別稱
量測,分別稱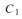 與
與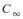 。其分別對應於以不同方式量測到之 A 的
Norm。
。其分別對應於以不同方式量測到之 A 的
Norm。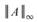 與
與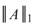 的計算採用如下定義(與線性代數教科書略有不同):
的計算採用如下定義(與線性代數教科書略有不同):
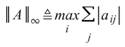 ,其中 i、j 為列與行的 Index。
,其中 i、j 為列與行的 Index。
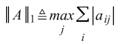 。
。
Condition Number 的意義:
(1)用來量度 A 的 Stiffness : 也就是特徵值 ( eigen-value )
的大小分佈狀況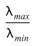 。
。
(2) 線性方程組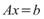 解對於機器誤差(round-off
error)的敏感度。也就是說當 b 稍微改變時,x 變化的程度。
解對於機器誤差(round-off
error)的敏感度。也就是說當 b 稍微改變時,x 變化的程度。
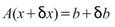 。
。
註:A 必需為一方陣。若 A 不為方陣時可用 SVD 法求得,但目前版本並不支援這項計算。
參數設定(Properties)
本模組接受實數(real number)、複數(complex number)、Numeric的數值資料,而輸出在 Properties 的 Reporter。
範例(Example)
-
以DoMatlab 模組製造亂數 A 的方陣:
矩陣內容如下:

若其 Condition Number 很接近零,則矩陣是 Singular,反矩陣不存在。
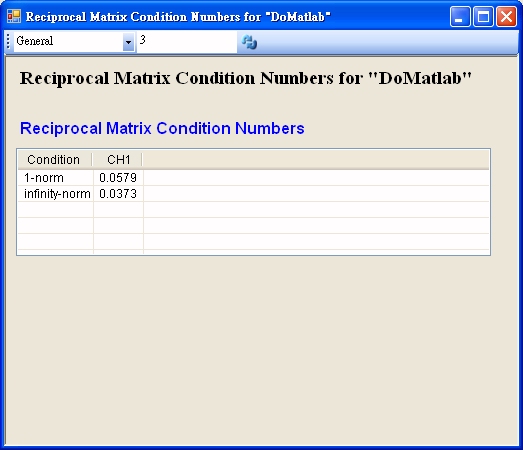
以本模組檢測之
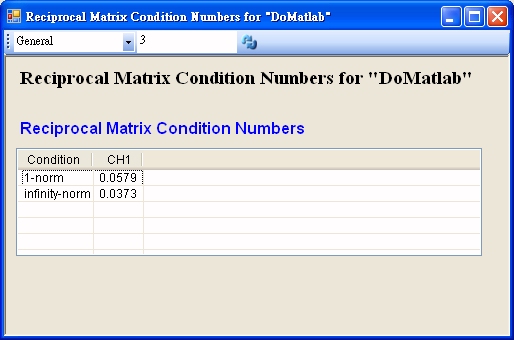
發現 Norm 的值並不是非常接近零,所以其反矩陣是存在的。( 可以 Inverse 模組計算之 )
相關指令
Matrix Inverse, Matrix Operation
參考
Gilbert Strang: Linear Algebra and Its Applications 3rd edition