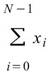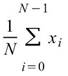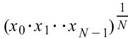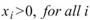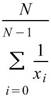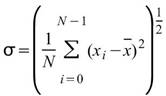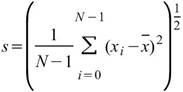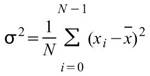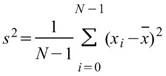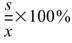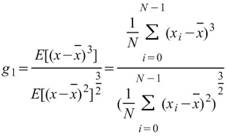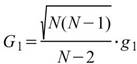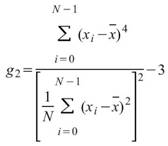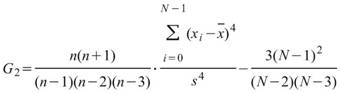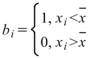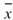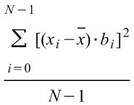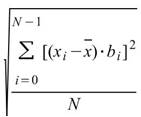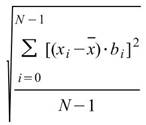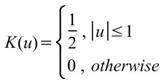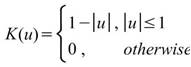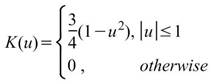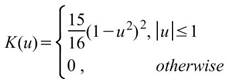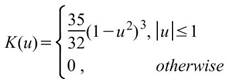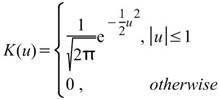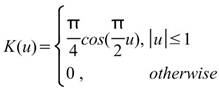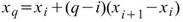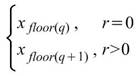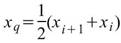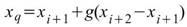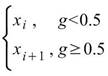*This module is available in Professional only*
本模組群提供計算訊號各項統計值之工具,包含的模組如下:
-
Basic Statistics:計算訊號之基本統計參數,諸如最大值、最小值、平均、標準差等。
-
Covariance Matrix:計算多筆訊號之共變異數矩陣。
-
Correlation Matrix:計算多筆訊號之相關係數矩陣。
-
Equiphase Statistics:計算輸入訊號之等相位統計值。
-
Kernel Smoothing Density:利用特定之核函數(kernel funciton)計算出輸入訊號之機率密度線,並可平滑之。
-
Orthogonality Matrix:對多筆訊號計算出彼此之正交性矩陣。
-
Quartiles and Quantiles:可計算訊號之各種分位數與四分位數。
-
Rolling Statistics:計算訊號之滾動統計值。
-
Hypothesis Test:對資料及訊號進行設定假設、選擇檢定方法、判斷是否接受假設。
-
Least Sqare Fitting:以最小平方法對訊號做回歸曲線,從一組時間序列或兩組時間序列中的找出最佳的相關曲線。
*Only in Professional*
Basic statistics 是一項讓使用者能快速檢視輸入數列之基本統計數據的工具。
說明:
令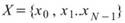 代表長度為 N 的數列(不限定為時間序列), Basic
Statistics 將計算下列各項統計資訊。
代表長度為 N 的數列(不限定為時間序列), Basic
Statistics 將計算下列各項統計資訊。
|
統計值 |
數學式 |
說明 |
|
Sum |
|
資料中每個元素的總合。 |
|
Min |
- |
資料中的最小值。 |
|
Max |
- |
資料中的最大值。 |
|
Mean |
|
計算資料算數平均值。 |
|
Geometric Mean |
|
計算資料幾何平均值,多用於計算比率、人口成長等呈幾何變化的數列。 |
|
Harmonic Mean |
|
計算調合平均數,多用於計算平均速率。 |
|
Trimmed Mean |
- |
截頭尾平均數,算法為先設定的濾除比例 ( % ),將資料X 排序後,頭尾各濾除比列的部份的數列部份濾除,剩下的訊號值作算數平均,如此可排除數列中極端值所造成的影響。 |
|
Median |
- |
資料的中位數。 |
|
StdDev |
|
標準差,可推估母體資料距離平均值的離散程度,假設此資料為樣本,無法利用樣本去推估母體標準差 ( Biased Moment Estimation)。 |
|
|
當此資料為樣本,計算樣本不偏估之標準差 ( Unbiased Moment Estimation ),可以用來推估母體標準差。 |
|
|
Variance |
|
母體資料的變異數 (標準差的平方),假設此資料為樣本,無法利用樣本去推估母體變異數( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之變異數 ( UnbiasedMoment Estimation ),可以用來推估母體變異數。 |
|
|
Coefficient of Variation |
|
母體變異係數,表示標準差佔平均值的百分比,用於比較多組資料個別間的離散程度 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之變異係數 ( Unbiased Moment Estimation ),可以用來推估母體變異係數。 |
|
|
Skewness |
|
母體偏度,用以推估資料分佈圖形的對稱性,即第三中央慣性矩除以標準偏差的三次方 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之偏度 (Unbiased Moment Estimation ),可以用來推估母體偏度。 |
|
|
Kurtosis |
|
母體峰度,用來推估資料分佈圖形是高瘦或者是矮胖,即第四中央慣性矩除以標準偏差的四次方減3 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之峰度 ( Unbiased Moment Estimation ),可以用來推估母體峰度。 |
|
|
Semivariance |
|
計算母體資料之半變異數,預設以數列平均值 |
|
|
當此資料為樣本,計算樣本不偏估之樣本半變異數( Unbiased Moment Estimation ),可以用來推估母體之半變異數。 |
|
|
Semi Standard Deviation |
|
將母體資料之半變異數 (Biased Moment Estimation ) 開根號即為資料之半標準偏差 ( Biased Moment Estimation )。 |
|
|
當此資料為樣本,計算樣本不偏估之樣本半標準差( Unbiased Moment Estimation ),可以用來推估母體半標準差。 |
參數設定(Properties)
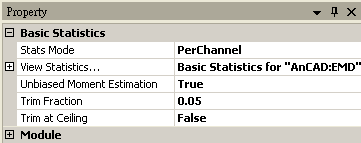
本模組接受實數(real number)、複數(complex number),單通道(single channel)或多通道(multi-channel),regular的訊號 ( signal ) 輸入,相關參數定義詳列如下表。
|
參數名稱 |
參數定義 |
預設值 |
|
Stats Mode |
如果輸入訊號為多通道,此參數將會被開啟,包含PerChannel 和 AcrossChannel。 若如預設 PerChannel ,結果會為一個 15 * n 的矩陣,其中 n 為輸入的 channel 數,15 個值為計算的統計值,輸出格式是 Indexed 的數值資料。 若設定為 AcrossChannel,計算同一個時間點下,輸入訊號中所有通道的 15 個統計值,最後輸出一個多通道訊號包含 15 個 channel ,長度跟輸入訊號相同。 |
PerChannel |
|
View Statistics… |
開啟 Reporter 視窗顯示模組元件計算結果。 |
無 |
|
Unbiased Moment Estimation |
如果輸入資料為樣本 (Sample),則選擇 True (Unbiased Moment Estimation) 進行統計量修正,進一步去推估母體 (Population) 的統計量。 反之若資料為母體 (Population),即可以設定 False ( biased Moment Estimation ),計算母體統計量 |
True |
|
Trimmed Fraction |
截頭尾平均的截去比例,以百分比表示%。 |
0.05 |
|
Trimmed at Ceiling |
當截去比例下之資料點位置為小數點時,選擇取前一點(參數設為 False )或是後一點(參數設為 True )作為 Trimmed 的點數。 |
False |
範例(Example)
計算白色雜訊與方波的基本統計分析:
-
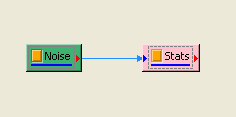
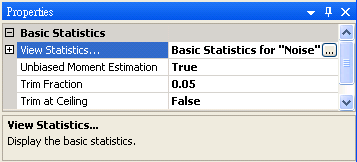
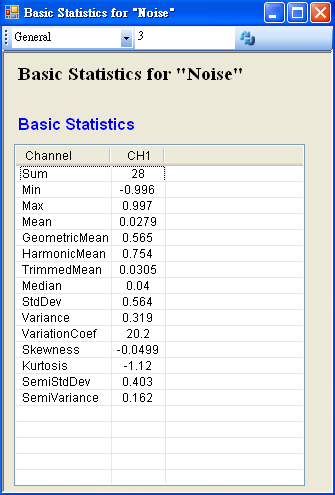
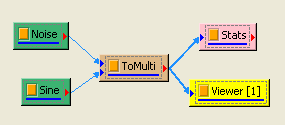
於 Network 視窗下選擇 Source / Noise 創造一個雜訊(預設為白色雜訊),後接上 Compute / Statistics / Basic Statistics,再點選 Basic Statistics 的 Properties / View Statistics…顯示計算結果。
-
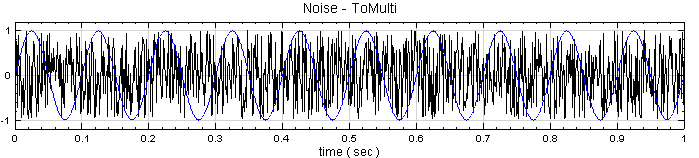
另新增一正弦波,用 Conversion / Merge to multi-channel 將此波與 Noise 結合為 Multi-channel 訊號,先以 Viewer / Channel viewer 繪製結果,再拉入 Stats,點選 Basic Statistics 的 Properties / ViewStatistics…,Basic Statistics 視窗即更新如下。
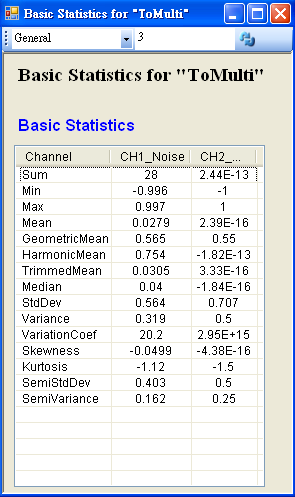
-
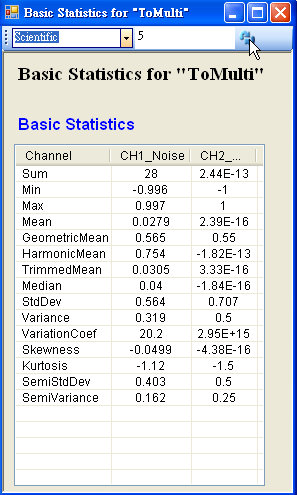
設定 Basic Statistics 工具列上的參數,使數值顯示為 Scientific,小數點位數調整為 5 位,最後記得按 Refresh 鈕更新,其結果顯示如下。
-
另外在一個新的專案中,Source / Noise 產生一個 White Noise,再將其接至 HHT / RCADA EEMD,最後以 Channel Viewer 觀看其結果。

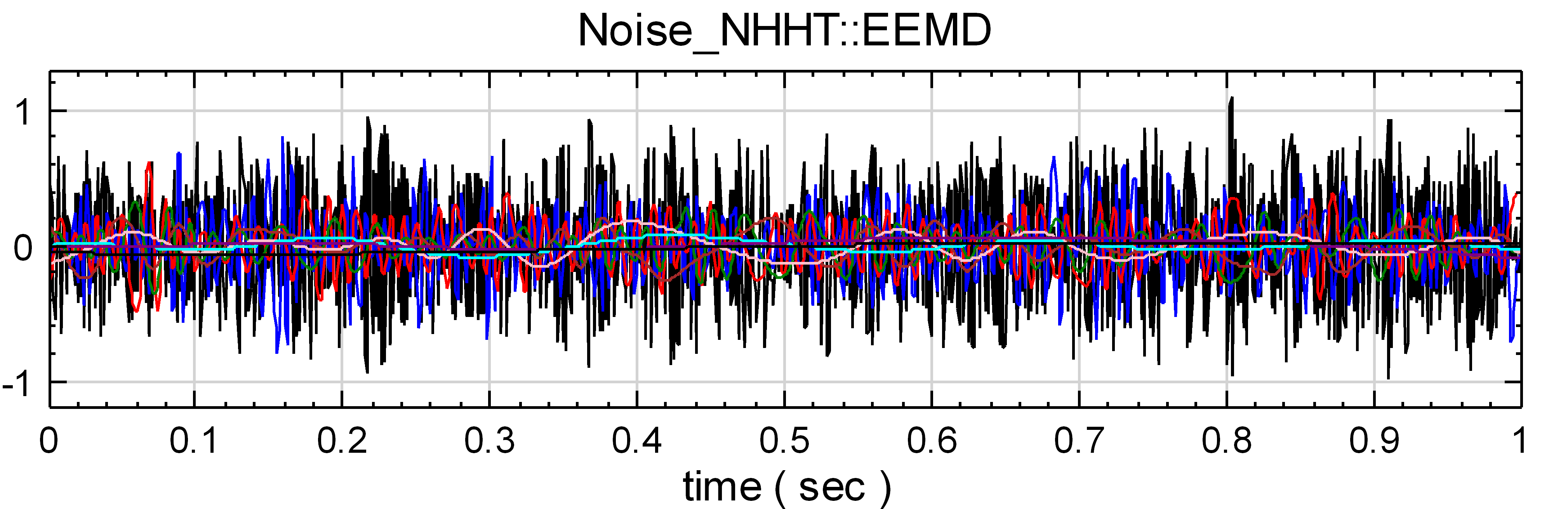
-
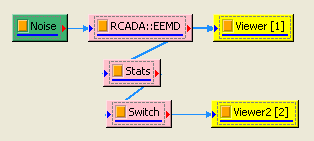
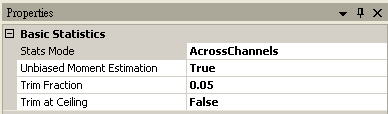
最後再將 RCADA EEMD 連接至 Compute / Statistics / Basic Statistics,然後 Properties / Stats Mode 選擇 AcrossChannels, 最後以連接 Compute / Channel / Channel Switch, Channel Viewer觀看其結果,可以利用 Channel Switch 選擇不同通道,檢視不同的統計量。
相關指令
Equiphase Statistics,Rolling Statistics,Merge to Multi。
參考
Michel Loeve, "Probability Theory", Graduate Texts in Mathematics, Volume 45, 4th edition, Springer-Verlaf, 1977
Joanes, D. N.&Gill, C. A.(1998) Comparing measuresof sample skewness and kurtosis. Journal of the Royal Statistical Society (Series D): The Statistician 47 (1), 183–189.
*Only in Professional*
共變異數是計算兩組數列各自對其平均值的變化相關程度,若值為正,代表兩數列呈正相關,值為負代表兩數列呈負相關。倘若有多比數列資料互相比較,則可將各資料對應之共變異數組成一個共變異數矩陣。
說明
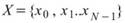 ,
,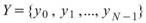 為兩組數列,則總量之共變異數(Covariance)計算如下:
為兩組數列,則總量之共變異數(Covariance)計算如下:
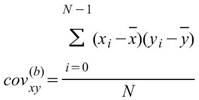
其中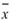 、
、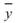 分別為兩數列的平均值。若考慮樣本不偏估之估計量(Unbiased
estimator),則方程式為
分別為兩數列的平均值。若考慮樣本不偏估之估計量(Unbiased
estimator),則方程式為
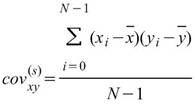
若有一組多通道(multi-channel)的數列,通道數為 M,則各通道間對應的總量/樣本相關係數可表示為共變異數矩陣。
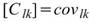 ,其中 l,k 為數列通道編號。
,其中 l,k 為數列通道編號。
其中矩陣的對角項(Diagonal terms)就是該通道數列的變異數,即:
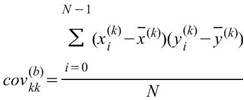
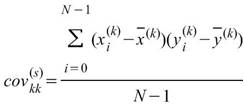
參數設定(Properties)
本模組接受實數(real number),多通道(multi-channel),regular 的訊號 ( signal ) 輸入。輸出為一個 M x M 的方形矩陣,其中 M 為通道數,輸出格式是 Indexed 的數值資料。計算結果於 Properties / View Matrix… 即可開啟 Reporter 視窗看到。

參數為 Unbiased Moment Estimation,可選擇是否計算樣本不偏估之共變異數矩陣,預設為“False”。
範例(Example)
以不同相位角與頻率的正弦波為輸入訊號計算其相關係數矩陣:
-
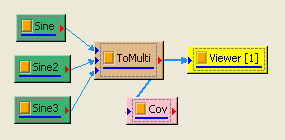
於 Network 視窗下按右鍵,選擇Source / Sine Wave 創造一個正弦波,此波預設頻率為 10Hz,接著再創造兩個正弦波,一個波設定其 Properties / SignalFreq = 5Hz,另一個波設定其 Properties / Phase=180 度(單位為Degree),最後使用 Conversion / Merge to Multi-channel 將三個訊號結合成一個 Multi-Channel 的訊號。以上步驟將創造一個頻率為 10Hz 的正弦波,頻率為 5Hz 的正弦波以及相位角偏移 180 度 的正弦波。以Viewer / Channel Viewer 繪出結果,其中黑線代表Sine,藍線代表 Sine2,紅線代表 Sine3。
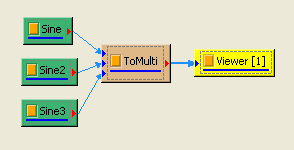
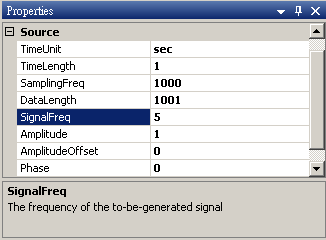
Sine2 的參數設定如下圖。
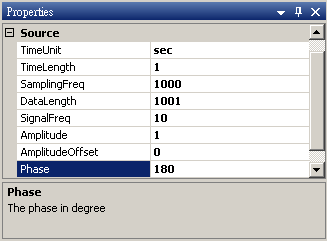
Sine3 Properties
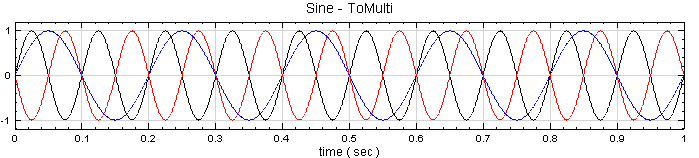
-
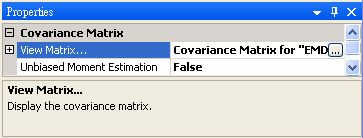
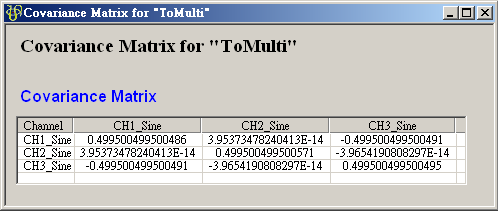
在 ToMulti 後方接上 Compute / Statistics / Covariance Matrix,點選其 Properties / View Matrix… 跳出計算結果。矩陣元素
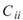 為各訊號對自己的共變異數,也就是各訊號的變異數約
0.499,
為各訊號對自己的共變異數,也就是各訊號的變異數約
0.499,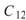 、
、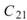 是 Sine 與 Sine2
的比較,其值極小,表示兩訊號無相關性,
是 Sine 與 Sine2
的比較,其值極小,表示兩訊號無相關性,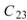 、
、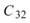 同樣為極小值,同理 Sine與 Sine2
也是無相關性;Sine 與 Sine3 為與 X 軸對稱的兩數列,其計算結果為 -0.499,代表兩訊號為負相關。
同樣為極小值,同理 Sine與 Sine2
也是無相關性;Sine 與 Sine3 為與 X 軸對稱的兩數列,其計算結果為 -0.499,代表兩訊號為負相關。
-
再開一個新的專案,以 Source / Triangle Wave 產生一組三角波,再接上 Compute / HHT / RCADA EEMD 計算出三角波的 IMF,計算結果以 Channel Viewer 繪出。Viewer 的 Properties / Multi-channel Display 調為 List,Viewer Height 調為 350,可以看到共分出 10 個通道的訊號。
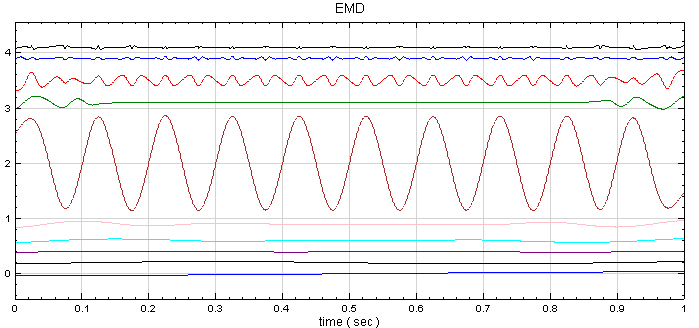
-
於 RCADAEEMD 後面再接上Compute / Statistics / Covariance Matrix,計算各 IMF 之間的共變異數矩陣。
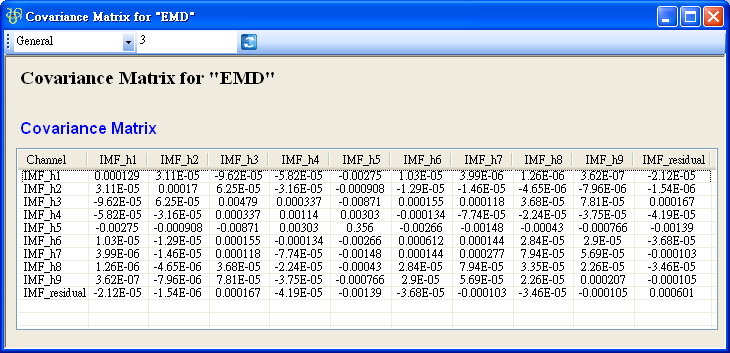
共變異數值的大小可衡量兩數列值變化的程度,值為正代表兩數列值相對於平均的變化趨勢相同,為正的線性相關,值為負代表兩數列值相對於平均的變化趨勢相反,為負的線性相關。另外可注意到矩陣的對角項為各通道的變異數。
相關指令
Correlation Matrix,Orthogonality Matrix,Merge To Multi-Channel,RCADA EEMD。
參考
N.G. van Kampen, Stochastic processes in physics and chemistry. New York: North-Holland, 1981.
*Only in Professional*
相關係數(Correlation Coefficient)即是正規化的共變異數,可指出兩組數列的相關程度,倘若有多筆數列相互交差比較,則可將各相關係數組成相關係數矩陣。
說明
令 ,
,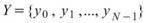 為兩組數列,則相關係數(Correlation
Coefficient)之計算如下:
為兩組數列,則相關係數(Correlation
Coefficient)之計算如下:
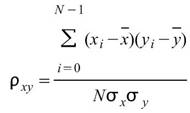
其中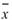 、
、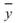 分別為兩數列的平均值,
分別為兩數列的平均值,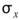 、
、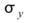 分別為兩數列的標準偏差。若考慮樣本不偏估之估計量(Unbiased
Moment estimator),則方程式為
分別為兩數列的標準偏差。若考慮樣本不偏估之估計量(Unbiased
Moment estimator),則方程式為
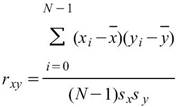
其中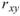 為兩樣本數列的相關係數,
為兩樣本數列的相關係數,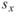 、
、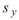 分別為兩數列的樣本標準偏差。相關係數之定義可視為共變異數除以兩數列之標準偏差。若有一組多通道(multi-channel)的數列,通道數為
M,則各通道間對應的總量 / 樣本相關係數可表示為相關係數矩陣。
分別為兩數列的樣本標準偏差。相關係數之定義可視為共變異數除以兩數列之標準偏差。若有一組多通道(multi-channel)的數列,通道數為
M,則各通道間對應的總量 / 樣本相關係數可表示為相關係數矩陣。
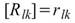
其中l,k 為通道代碼。
參數設定(Properties)
本模組接受實數(real number),多通道(multi-channel),regular的訊號(signal)輸入。輸出為一個 M x M 的方形矩陣,M 為channel數,輸出格式是 Indexed 的數值資料。於 Properties / View Matrix… 即可用Reporter視窗看到計算結果。
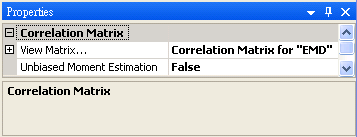
參數為 Unbiased Moment Estimation,可選擇是否計算樣本不偏估之相關係數矩陣,預設為 " False "。
範例(Example)
以不同相位角與頻率的正弦波為輸入訊號計算其相關係數矩陣結果:
-
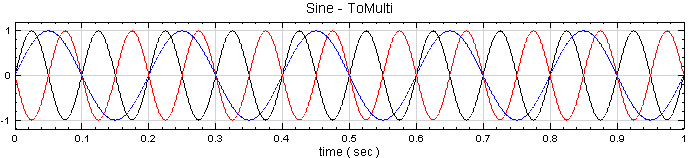
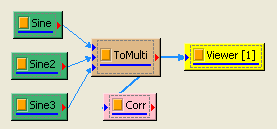
於 Network 視窗下按右鍵,選擇 Source / Sine Wave 創造一個正弦波,此波預設頻率為 10Hz,接著再創造兩個正弦波,一個波設定其Properties / SignalFreq = 5Hz,另一個波設定其 Properties / Phase = 180 度(單位為Degree),最後使用 Conversion/Merge to Multi-channel 將三個波結合成一個 Multi-Channel 的訊號。以上步驟將創造一個頻率為 10Hz 的正弦波,頻率為 5Hz 的正弦波以及相位角偏移 180 度的正弦波。以 Viewer / Channel Viewer 繪出結果,其中黑線代表Sine,藍線代表Sine2,紅線代表Sine3。

Sine2 Properties
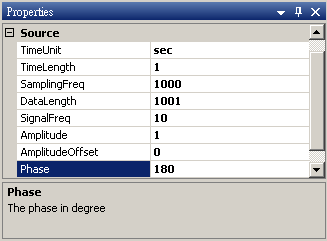
Sine3 Properties
-
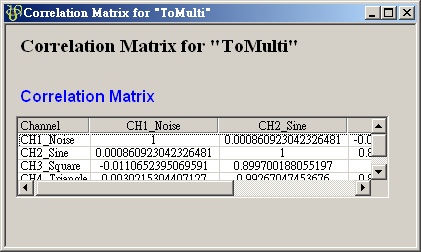
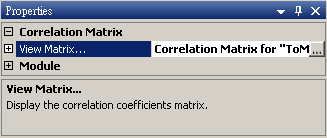
在 ToMulti 後方接上 Compute / Statistics / Correlation Matrix,點選其 Properties / View Matrix… 跳出計算結果。矩陣對角項
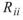 為各訊號對自己的相關係數,因此為 1
完全相關,
為各訊號對自己的相關係數,因此為 1
完全相關,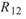 、
、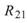 是 Sine 與 Sine2
的比較,其值約為
是 Sine 與 Sine2
的比較,其值約為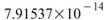 ,表示兩訊號無相關性,
,表示兩訊號無相關性,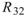 、
、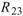 同樣為極小值,同理 Sine 與 Sine2
也是無相關性;Sine 與 Sine3 為與x軸對稱的兩數列,其計算結果為 -1,代表完全負相關。
同樣為極小值,同理 Sine 與 Sine2
也是無相關性;Sine 與 Sine3 為與x軸對稱的兩數列,其計算結果為 -1,代表完全負相關。
-
再開一個新的專案,以 Source / Triangle Wave 產生一組三角波,再接上 Compute / HHT / RCADA EMD 計算出三角波的 IMF,計算結果以 Channel Viewer 繪出。Viewer 的 Properties / Multi-channel Display 調為 List,Viewer Height 調為 350,可以看到共分出 10 個通道的訊號。

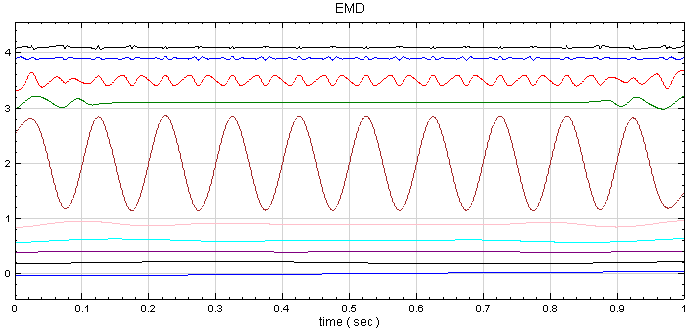
-
於 RCADA EMD 後面再接上出 Compute / Statistics / Correlation Matrix,這樣可計算出各 IMF 之間的相關係數。

矩陣的對角項為各通道對自己的相關係數,所以等於 1;除了對角項之外,值最大的相關係數為 IMF_h5 與 IMF_h1,表示這兩組訊號有較強的相關性,其餘大多數的相關係數值都小於正負 0.1,代表其餘 IMF 彼此間的相關性很小。
相關指令
Covariance Matrix,OrthogonalityMatrix,Merge To Multi-Channel,Channel Viewer,RCADA EMD。
參考
Cohen, J., Cohen P., West, S.G.,&Aiken, L.S. (2003). Applied multiple regression/correlation analysis forthe behavioral sciences. (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associmtes.
*Only in Professional*
等相位統計值,為設定一段長度為 M 的週期,在此週期下計算每個同相位元素的統計值,譬如計算月均值,週均值等,此計算方式即為 Equiphase Statistics。
說明
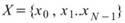 為一組個數為 N 的數列,而 Equiphase
Statistics 所設定的週期大小為 M,M<N,則此數列可分作 K = Ceiling ( N / M )
個小數列,Ceiling 表示小數點後無條件進位,令小數列為
為一組個數為 N 的數列,而 Equiphase
Statistics 所設定的週期大小為 M,M<N,則此數列可分作 K = Ceiling ( N / M )
個小數列,Ceiling 表示小數點後無條件進位,令小數列為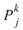 ,k 標示小數列編號,j 標示數列內之元素,則
,k 標示小數列編號,j 標示數列內之元素,則
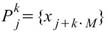 ,
,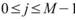 ,
,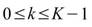 (如下圖所示)
(如下圖所示)
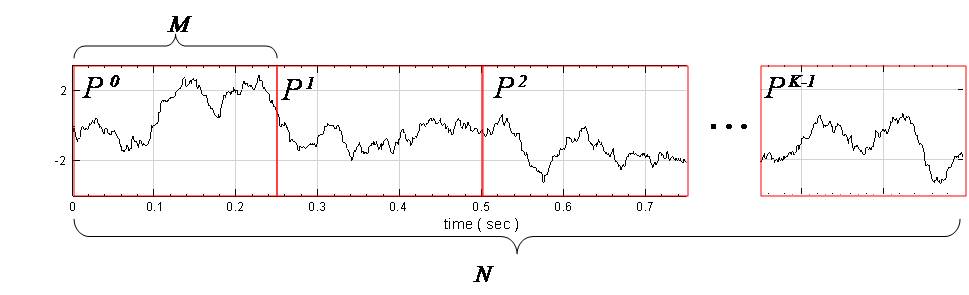
EquiphaseStatistics 就是抽出每個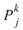 中相同相位的元素作為一組,計算其統計值,譬如
equiphase mean 的計算如下。
中相同相位的元素作為一組,計算其統計值,譬如
equiphase mean 的計算如下。
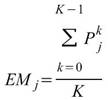 ,
,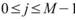 。
。
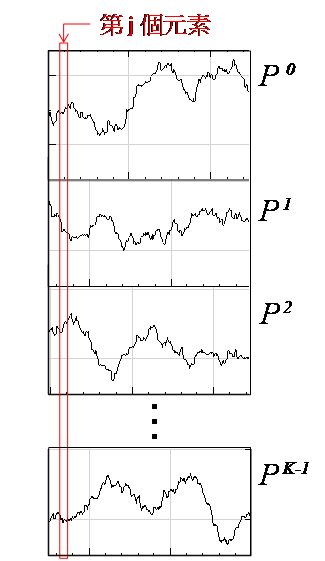
須注意當 N / M 不整除時,最後一組小數列長度 M_last<N,因此當相位元素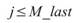 時,計算之元素數量為 K,當元素 j>M_last
時,計算元素數量為 K-1。
時,計算之元素數量為 K,當元素 j>M_last
時,計算元素數量為 K-1。
Equiphase statistics 可計算多種統計值,其中大部份與 Basic statistics 模組相同,此處不再贅述,算式請參照 Basic statistics 內容,其它部份,譬如 First quartile、Third quartile 與 Quantile 的詳細定義請參考 Quartiles and Quantiles 模組。
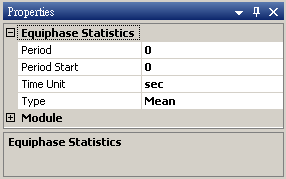
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入。參數定義如下。
|
參數名稱 |
參數定義 |
預設值 |
|
Period |
設定週期,單位為時間。 |
輸入訊號時間總長的百分之十 |
|
Period Start |
設定起始點位置,單位為時間。 |
0 |
|
TimeUnit |
時間單位。 |
sec |
|
Type |
設定要計算的統計量。 |
Mean |
Type選項定義如下,計算於窗內範圍的統計量。
|
選項名稱 |
選項定義 |
|
Sum |
數列總合。 |
|
Min |
數列中最小值。 |
|
Max |
數列中最大值。 |
|
Mean |
平均值。 |
|
Geometric Mean |
幾合平均數。 |
|
Harmonic Mean |
調合平均數。 |
|
Trimmed Mean |
截尾平均數。 |
|
First quartile |
數列值四分位值。 |
|
Median |
數列的中位數。 |
|
Third quartile |
數列的四分之三位值。 |
|
Quantile |
數列的分位數。 |
|
StdDev |
數列的標準偏差。 |
|
Variance |
數列的變異數。 |
|
VarianceCoef |
變異係數。 |
|
Skewness |
數列的偏度。 |
|
Kurtosis |
數列的峰度。 |
|
SemiVariance |
半變異數。 |
|
SemiStdDev |
半標準偏差。 |
部分選項會再出現參數需要設定,Quantile 的參數請參閱 Quartiles and Quantiles 模組說明,其餘統計量的定義請參考模組Basic Statistics內容。
範例(Example)
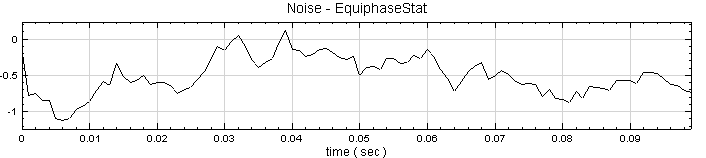
以一組 Brownian Noise 為輸入訊號,計算 Equiphase Statistics 的各項統計值。
-
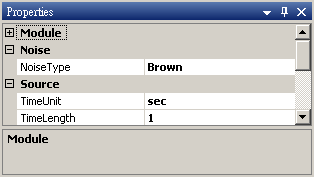
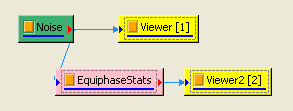
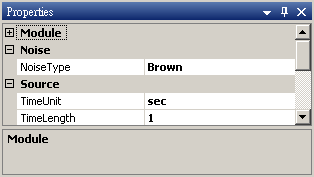
於 Network 按右鍵新增 Source / Noise,調整 Properties / Noise Type 為 Brown,以 Viewer / ChannelViewer 繪出結果。

-
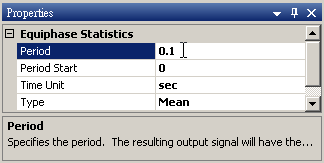
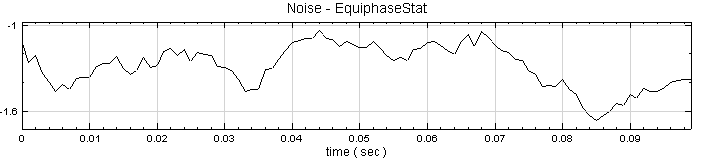
於 Noise後方接 Compute / Statistics / Equiphase Statistics,其統計值預設為 Mean,調整 Properties / Period 為 0.1,讓它以 0.1秒為週期,計算該週期下每個元素的平均值。最後以 Viewer / Channel Viewer 輸出結果。
-
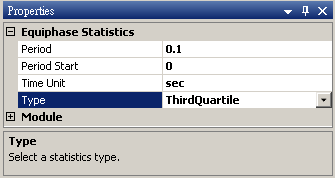
調整 Type 為 Third Quartile,則模組會計算週期下每個元素位置的四分之三位值。
相關指令
Basic Statistics,Rolling Statistics,Quartilesand Quantiles, Channel Viewer。
參考
1. Michel Loeve, "Probability Theory", Graduate Texts in Mathematics, Volume 45, 4th edition, Springer-Verlaf, 1977
2. Joanes, D. N.&Gill, C. A. (1998)Comparing measures on sampleskewness and kurtosis. Journal of the Royal Statistical Society (Series D): The Statistician 47 (1), 183–189.
*Only in Professional*
Kernel smoothing density estimation 是以非參數化(non-parametric)的方法計算出數列的機率密度函數( probability density function )。
說明
設數列為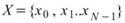 ,則數列的 kernel density
estimation 為:
,則數列的 kernel density
estimation 為:
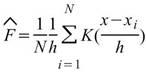
其中 h 是控制平滑程度的參數,即平滑窗 ( smoothing window ) 的長度,K 是核函數 ( kernel function )。此方法是將離散分佈之每個點代入核函數中,再疊加每個點的核函數計算結果,以達到平滑之目地。在概念上與作統計直方圖類似。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)輸入;輸出訊號格式為實數,多通道,regular的訊號。
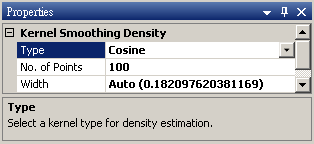
參數定義整理如下表。須注意 KS Density 輸出的訊號格式,一組輸入訊號會產生一組兩個通道的輸出訊號,第一個通道為 X 軸資料,以資料的極大及極小為上下界限,第二個通道為 Y 軸資料,為數列數值相對應之機率密度值。
|
參數名稱 |
參數定義 |
預設值 |
|
Type |
核函數的種類,內建函數包括Uniform、Triangle、Epanechnikov、Quartic、Triweight、Gaussian、Cosine,其定義整理至下一個表格中。 |
Gaussian |
|
No. of Points |
輸出訊號之離散點數。 |
100 |
|
Width |
平滑窗之寬度, 即 h,為控制平滑程度的常數,預設值 Auto 是假設標準常態分佈下計算最佳的寬度。 |
Auto |
下表整理常見核函數之定義。
|
核函數名稱 |
定義 |
|
Uniform |
|
|
Triangle |
|
|
Epanechnikov |
|
|
Quartic |
|
|
Triweight |
|
|
Gaussian |
|
|
Cosine |
|
範例(Example)
-
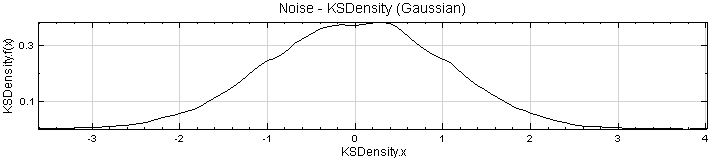
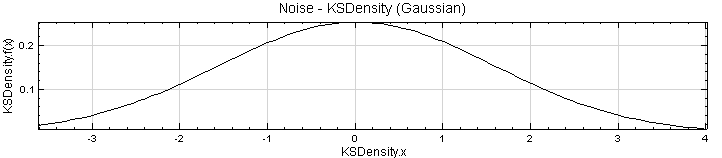
建立一個 Source / Noise,調整其 Properties/Noise Type 為 Gaussian,Time Length 設為 10 秒,再接上 Kernel Smooth Density,連結上 XY Plot。

-
另一方面將 Noise 直接以 Viewer / Histogram Viewer 繪出,將 Histogram 的 Properties / BinCount 調整為 50,Percentage 調為 True,則可畫出下面的直方圖。
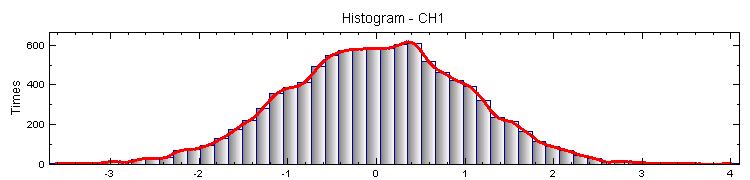
這兩張圖的基本概念是相同的,kernel smooth density 是以 kernel function 將數值出現的機率轉為連續的密度函數表示,而 histogram 是以值區間計算每個區間內數值發生的機率;且本模組所計算的密度函數其 X 軸以上的面積為 1,而 histogram 的 Y軸直接是發生次數。
將 KSDensity 的 Properties / Width 調大一點,調整到 1.2,可看到結果更為平順。
相關指令
Histogram,Noise,XY Plot。
參考
T. Hastie, R. Tibshirani and J. Friedman, The Elements of Stbtistical Learning, Chapter 6, Springer, 2001.
*Only in Professional*
正交性矩陣是計算數列間的正規化的內積 ( Dot Product ),若兩訊號正交,則其值為零,可以用在 EMD 計算的 IMF 上,判斷各 IMF 彼此間是否正交。
說明
令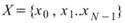 ,
,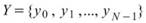 為兩組數列,則其正交性定義為兩數列的內積,計算如下:
為兩組數列,則其正交性定義為兩數列的內積,計算如下:
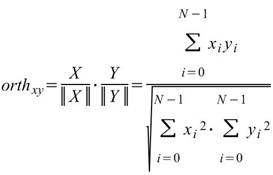
若有 M組數列,與其對應的正交性矩陣表示如下:
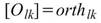 ,其中 l,k 為通道編號。
,其中 l,k 為通道編號。
參數設定(Properties)
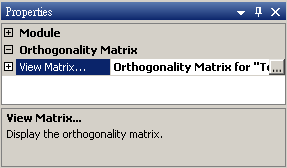
本模組接受實數(real number),多通道(multi-channel),regular的訊號(signal)輸入。輸出為一個 M x M 的方形矩陣,M 為輸入訊號的通道數,輸出格式是Indexed的數值資料。於Properties/View Matrix…即可用Reporter視窗看到計算結果。
範例(Example)
以不同相位角與頻率的正弦波為輸入訊號計算,正交性矩陣:
-
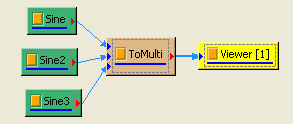
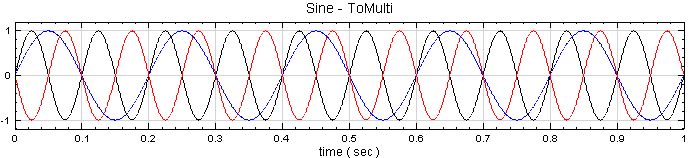
於 Network 視窗下按右鍵,選擇 Source / Sine Wave 創造一個正弦波,此波預設頻率為 10 Hz,接著再創造兩個正弦波,一個波設定其Properties / SignalFreq = 5Hz,另一個波設定其 Properties / Phase =180 度(單位為Degree),最後使用 Conversion / Merge to Multi-channel 將三個波結合成一個 Multi-Channel 的訊號。以上步驟將創造一個頻率為10Hz 的正弦波,頻率為 5Hz 的正弦波以及相位角偏移 180 度的正弦波。以 Viewer/ Channel Viewer 繪出結果,其中黑線代表Sine,藍線代表Sine2,紅線代表Sine3。
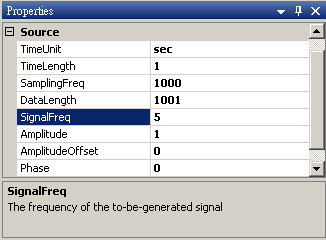
Sine2 Properties
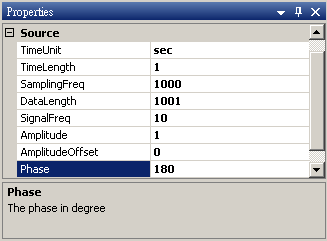
Sine3 Properties
-
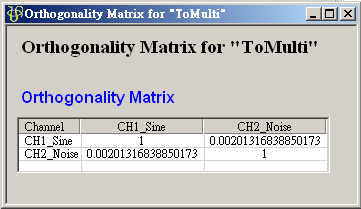
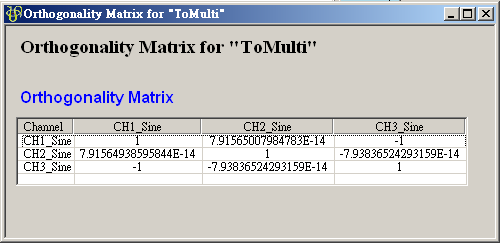
在 ToMulti 後方接上 Compute / Statistics / Orthogonality Matrix,點選其 Properties / View Matrix…跳出計算結果。矩陣對角項
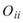 為各訊號對自己的正交性,也就是訊號對自己作內積,其值為1;
為各訊號對自己的正交性,也就是訊號對自己作內積,其值為1;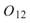 、
、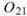 是
Sine 與 Sine2 的比較,其值極小,表示兩訊號相互正交,
是
Sine 與 Sine2 的比較,其值極小,表示兩訊號相互正交,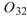 、
、 同樣為極小值,同理 Sine 與 Sine2
也是相互正交;Sine 與 Sine3 為對 X 軸對稱的兩數列,因此其計算結果為 -1。
同樣為極小值,同理 Sine 與 Sine2
也是相互正交;Sine 與 Sine3 為對 X 軸對稱的兩數列,因此其計算結果為 -1。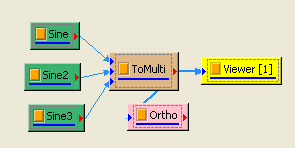
相關指令
Covariance Matrix,Correlation Matrix,Merge To Multi-Channel,Channel Viewer。
參考
Probability, Random Variables and Stochastic Processes. McGraw-Hill, 211.
*Only in Professional*
四分位數與分位數。分位數為一數列經排序後,其分佈位置占總量某個百分比的數值,而四分位數是在總量25%、50%、75%的位置的數值。
說明
令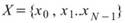 為一組個數為N的數列,則四分位數可表示為
為一組個數為N的數列,則四分位數可表示為
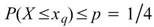 ,
,
若以較明確的說法,一數列的四分位數是其累積分佈函數等於 25% 的數值,位置 q 在 N * 25% - 1 處,中位數與四分之三位數也是相同的概念。分位數 Quantile 則是更一般化的分位數,以百分比為標準,如 17 位數(17thquantile) 代表在數列中累積分佈函數等於17%的數值。
若估計分位數時,該分位位置在兩點之間(即 q = N * p - 1 不為整數),則需要推估該分位的位置,估計方法眾多,本元件整理五種較常用的計算式供使用者選擇。
|
內插方法 |
定義 |
說明 |
|
Linear |
其中 i 代表 q 的整數部分 |
分位位置的前一點與下一點的數值作線性內插計算分位數。 |
|
Next point |
|
以分位位置下一點的數值當作分位數。 |
|
Average |
|
分位位置的前一點與下一點的數值取平均作為該分位數。 |
|
Weighted Average |
其中 i 是 ( N-1 ) * p 的整數部份,g 是小數部份。 |
分位位置的前一點加上前後兩點之差的加權值,此方法被Microsoft Office Excel 所採用。 |
|
Nearest |
其中 i 是 ( N-1 ) * p 的整數部份,g 是小數部份。 |
離分位位置最近的位置作分位數。 |
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)輸入。
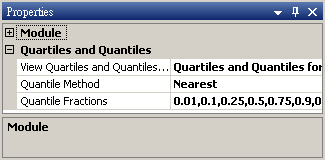
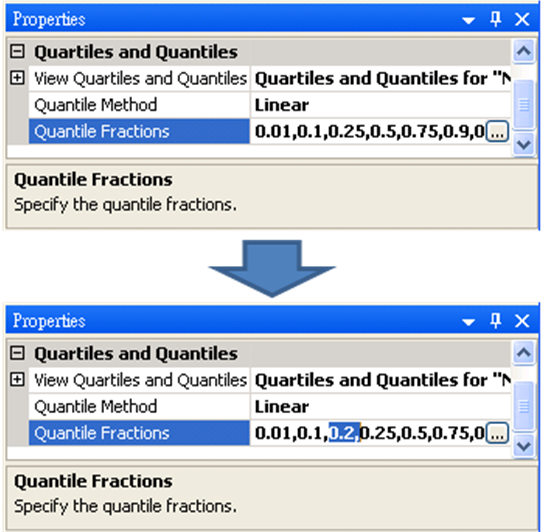
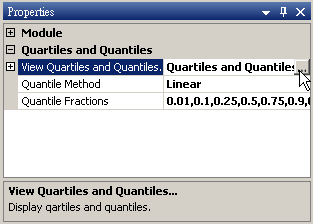
參數設定介面如下圖,本模組預設就計算數列的四分位數、中位數、四分之三位數等 Quartiles 值,另外可在參數 Quantile Fractions 下設定希望計算的 Quantiles 值。參數View Quartiles and Quantiles…會跳出視窗顯示計算結果。參數 Quantile Method 則可選擇 Quantile 的估計方法。下面就各參數內容分項說明。
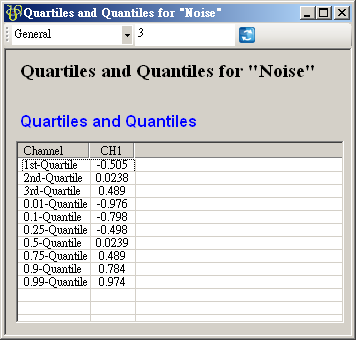
上圖為按下 View Quartiles and Quantiles… 右方![]() 鈕即跳出視窗,每一筆訊號的計算結果以 Column 為單位呈現,第一個 Column 顯示 Quartile
與 Quantile 名稱,第二 Column 之後每個 Column 都對應至輸入訊號每個 Channel,前三 Rows
計算三個四分位值,後面的 Rows 計算Quartiles,使用者利用參數 Quartile Fractions
來設定。下面將介紹參數 Quantile Fractions。
鈕即跳出視窗,每一筆訊號的計算結果以 Column 為單位呈現,第一個 Column 顯示 Quartile
與 Quantile 名稱,第二 Column 之後每個 Column 都對應至輸入訊號每個 Channel,前三 Rows
計算三個四分位值,後面的 Rows 計算Quartiles,使用者利用參數 Quartile Fractions
來設定。下面將介紹參數 Quantile Fractions。
Quantile Fractions 有兩種方式可以設定分位數。第一種方法是直接在欄位裡更改數據,譬如在0.1與0.25之間鍵入「0.2,」(如下圖),就可以新增分位數。
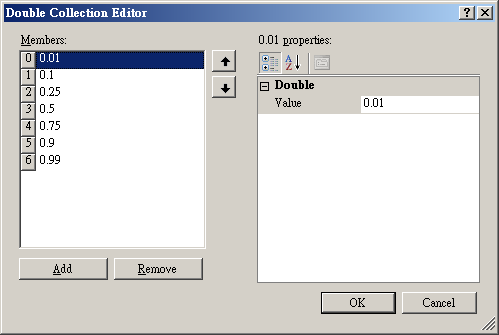
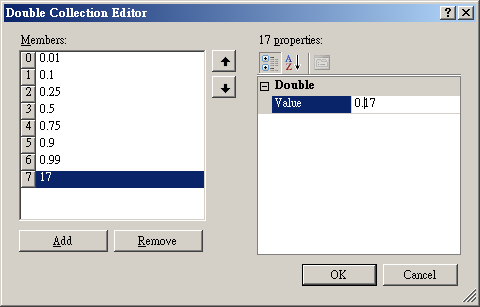
第二種方法是按下 Quantile Fractions 右方![]() 鈕,跳出分位數編輯視窗(如下圖),如果一次需要新增或移除很多個分位數,可以採取此作法。左邊為設定的
Quantile Member,使用者可以用下面的 Add / Remove 按鈕新增/移除計算項目,另外可以在右邊視窗編輯每個
Member 要計算的 Quantile 的比例,如 0.01 代表 1% Quantile,編輯完成後,按下 OK
鈕即完成設定。設定後這些 Quantiles 的計算結果會顯示在成 View Quartiles and
Quantiles…視窗中。
鈕,跳出分位數編輯視窗(如下圖),如果一次需要新增或移除很多個分位數,可以採取此作法。左邊為設定的
Quantile Member,使用者可以用下面的 Add / Remove 按鈕新增/移除計算項目,另外可以在右邊視窗編輯每個
Member 要計算的 Quantile 的比例,如 0.01 代表 1% Quantile,編輯完成後,按下 OK
鈕即完成設定。設定後這些 Quantiles 的計算結果會顯示在成 View Quartiles and
Quantiles…視窗中。
Quantile Method 內有五種方法,分別為 linear、next、mean、weighted mean、nearest,其估計原理在理論中都有詳述。
|
參數名稱 |
參數定義 |
預設值 |
|
View Quartiles and Quantiles |
顯示計算的 Quartiles 和 Quantiles結果。 |
無 |
|
Quantile Method |
Linear、Next、Mean、Weighted mean、Nearest。 |
Linear |
|
Quantile Fractions |
可設定多個 Quantile 的百分比。 |
[0.01; 0.1; 0.25; 0.5; 0.75; 0.9; 0.99] |
範例(Example)
以一組Brownian Noise為輸入訊號,計算 Quartiles 與 Quantiles。
-
於 Network 按右鍵新增 Source / Noise,調整 Properties / Noise Type 為 Brown,以Viewer / Channel Viewer 繪出結果。

-
於 Noise 後方接 Compute / Statistics / Quartiles and Quantiles 計算各項分位數值,點擊 Properties / View Quartiles and Quantiles…檢視結果。
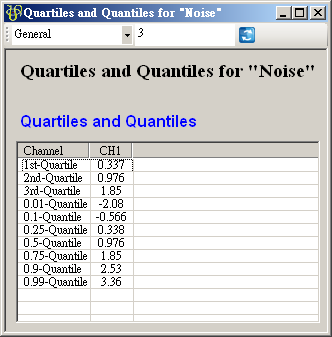
-
點選 Properties / Quantile Fractions 來編輯不同的分位值,按下編輯介面的 Add 按鈕(如下圖),會在 Members 處新增一個值為 0 的 member。
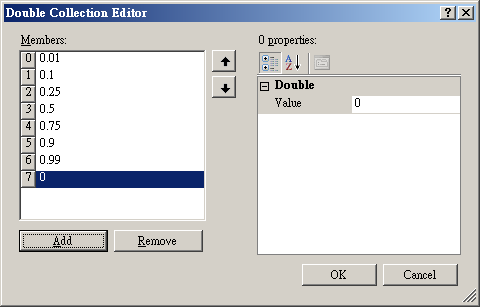
接下來,於編輯介面的右邊可設定分位數的百分比,譬如說設定為 0.17,完成後按下 OK 鈕。
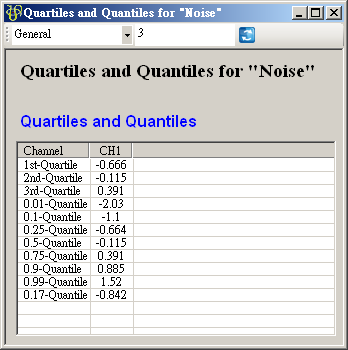
-
再次點選 View Quartiles and Quantiles…,可以看到已經新增了一個 17th Quantile。
相關指令
Basic Statistics,Rolling Statistics,Channel Viewer。
*Only in Professional*
滾動統計值,為設定一段元素數量為 M 的窗,統計函數計算窗內部份的統計值,譬如平均值,並且移動此窗以計算出的新的數列,此計算方式即為 Rolling statistics。
說明
令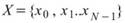 為一組個數為 N 的數列,而 rolling
statistics 所設定的窗
為一組個數為 N 的數列,而 rolling
statistics 所設定的窗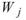 長度為
M,M<N,則此窗內的元素可表示為
長度為
M,M<N,則此窗內的元素可表示為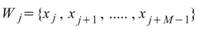 ,其中
,其中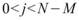 ,Rolling statistics
就是計算此窗內的統計值,譬如 Rolling mean
,Rolling statistics
就是計算此窗內的統計值,譬如 Rolling mean
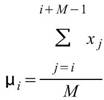 ,
,![]() 。
。
另外定義一個 overlap 值 ( p ) ,p 代表計算下一段窗時,有多少窗內的元素是與前一段重疊的。以 rolling means 為例,設定窗大小 M = 10,則輸出值第一點
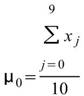 , 即下圖
, 即下圖
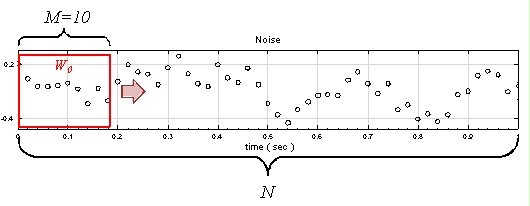
範圍是訊號位置 0 至 9 ,如上圖所示,若 p = 9,則計算下一段窗的範圍是在訊號位置 1至 10處,即
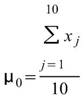
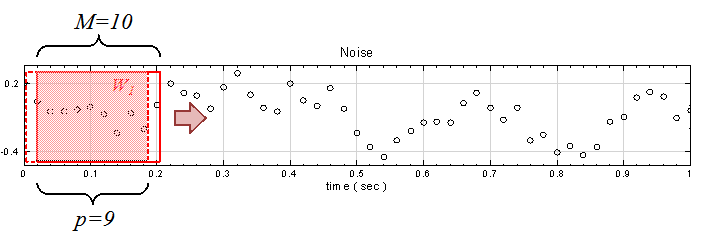
兩段相比有 9 個位置重疊。倘若 p = 7,則
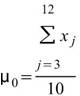 ,
,
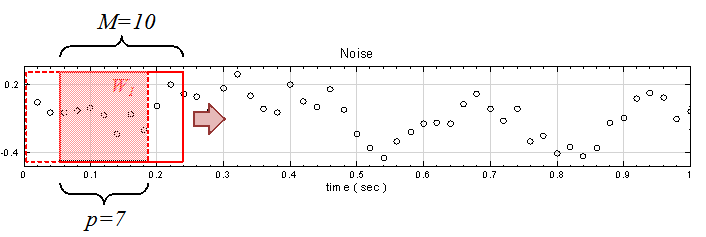
與前段相比有 7 個訊號位置重疊,以此類推,輸出數列的長度為
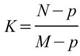 ,
,
須注意當 m - p>1 時,輸出數列的長度 K 可能無法整除的狀況,而處理方式為捨去餘數,僅保留完整的窗所計算的結果,因此
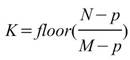 。
。
Rolling statistics 可計算某種統計值,項目與 Basic statistics 模組相同,此處不再贅述。
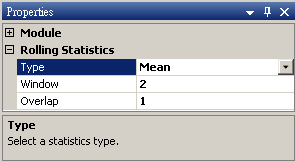
參數設定(Properties)
本模組接受實數(real number)、複數(complex number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)輸入。參數定義如下。
|
參數名稱 |
參數定義 |
預設值 |
|
Type |
可選擇想要計算的統計值,詳細清單可見下表。 |
Mean |
|
Window |
設定窗的大小,單位為訊號元素個數。 |
2 |
|
Overlap |
設定rolling時重疊元素的數量。 |
Window -1 |
Type選項定義如下,計算於窗內範圍的統計量。
|
選項名稱 |
選項定義 |
|
Sum |
計算總合。 |
|
Min |
數列中最小值。 |
|
Max |
數列中最大值。 |
|
Mean |
平均值。 |
|
Geometric Mean |
幾合平均數。 |
|
Harmonic Mean |
調合平均數。 |
|
Trimmed Mean |
截頭尾平均數。 |
|
First quartile |
數列的四分位值。 |
|
Median |
數列的中位數。 |
|
Third quartile |
數列的四分之三分位值。 |
|
Quantile |
數列的分位數。 |
|
StdDev |
數列的標準偏差。 |
|
Variance |
數列的變異數。 |
|
VarianceCoef |
變異係數。 |
|
Skewness |
數列的偏度。 |
|
Kurtosis |
數列的峰度。 |
|
Semivariance |
半變異數。 |
|
SemiStdDev |
半標準偏差。 |
部分選項會再出現參數需要設定,Trimmed Mean 請參考 Basic Statistics 說明文件,Quantile 的參數請參閱 Quartiles and Quantiles 說明文件,其餘統計量的定義請參考模組 Basic Statistics 內容。
範例(Example)
以一組 Brownian Noise 為輸入訊號,計算 rolling statistics 的各項統計值。
-
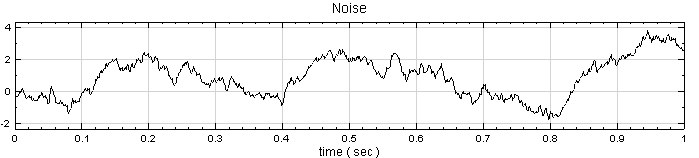
於 Network 按右鍵新增 Source / Noise,調整 Properties / Noise Type 為 Brown,以 Viewer / Channel Viewer 繪出結果。
-
於 Noise 後方接 Compute / Statistics / Rolling Statistics,其統計值預設為 Mean,window 預設為 2。以 Channel Viewer 輸出結果。
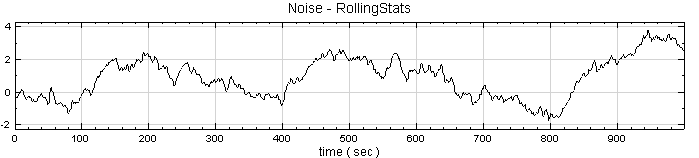
-
因為 window = 2,所以步驟2之計算結果與原訊號差異不大,調整 window 大小為 50,算出的結果如下圖所示;再點選 RollingStats 圖示,按 Network 工具列上 Data Viewer 功能看 Data count 長度,長度為 952,可套用理論中 K 值驗算。
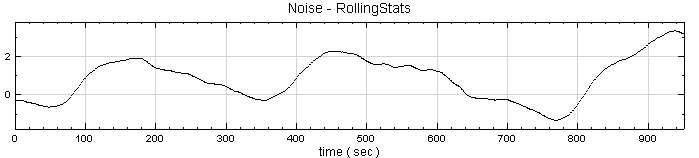
相關指令
Basic Statistics,Equiphase Statistics,Quartiles and Quantiles,Merge To Multi-Channel,Channel Viewer。
*Only in Professional*
先針對母體做出一個適當暫時性假設,再依據隨機樣本統計量的抽樣分配,定義出一個拒絕假設的標準,如果樣本統計量計算後落在拒絕區,則推翻原先建立之暫時性假設,否則必須接受暫時性假設。
理論(Theory)
實驗所得到數據包含機會誤差、真實誤差以及其他影響,利用假設檢定來解決這類問題。一般而言包含三個步驟,設定假設、選擇檢定方法、判斷是否接受假設。
虛無假設 ( Null Hypothesis ) : 實驗數據間的差異屬於機會誤差。
對例假設 ( Alternative Hypothesis ) : 實驗數據間的差異屬於真實誤差。
1. Z-test :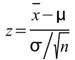
Z-test中 為輸入訊號的平均(樣本平均),
為輸入訊號的平均(樣本平均),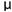 為假設母體平均,
為假設母體平均,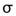 為母體標準差,
為母體標準差,
n 為輸入訊號數量(樣本數量)。
2. T-test :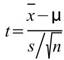
T-test中 為輸入訊號的平均(樣本平均),
為輸入訊號的平均(樣本平均),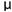 為假設母體平均,
為假設母體平均,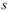 為樣本標準差,n 為輸入訊號數量(樣本數量)。
為樣本標準差,n 為輸入訊號數量(樣本數量)。
實驗過程中,進行重複相當多次的實驗,實驗結果的平均將會呈現常態分佈 ( 如下圖 ),若要檢驗某次實驗結果是否擁有機會誤差,可以利用Z-test、 T-test,計算出此次實驗平均結果座落常態分佈何處。研究者假設一個拒絕虛無假設範圍,( 以佔常態分佈面積的比例,又稱 Significant Level ),再依照檢定方法 Null (雙尾)、RightTail (右尾) 和 LeftTail (左尾) ( 如下圖 ),判斷實驗平均結果是否落入拒絕範圍。
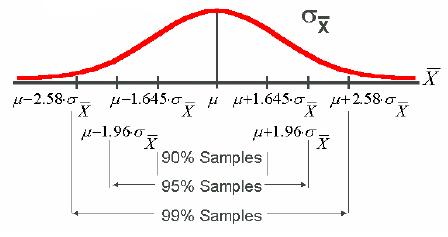
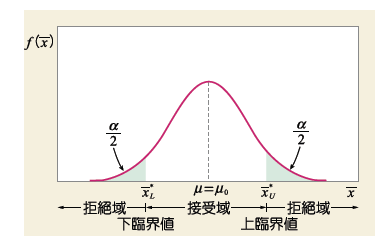
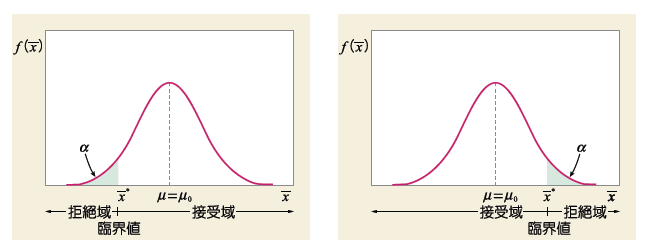
3.Var-Test (Chi-square variance test) :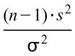
Var-test中 為樣本變異數,
為樣本變異數,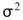 為母體變異數, n 為輸入訊號數量(樣本數量)。
為母體變異數, n 為輸入訊號數量(樣本數量)。
4.Runs-Test ( Runs test of Randomness, Geary test ):
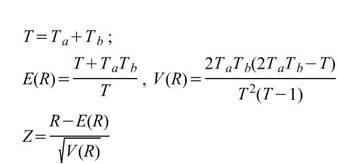
在 Runs-Test 中,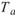 為樣本中大於樣本平均值的數量,
為樣本中大於樣本平均值的數量,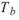 為樣本中小於樣本平均值的數量,R 為由 a , b
的交替出現次數,列如 aaabbaaba,則 R=5。
為樣本中小於樣本平均值的數量,R 為由 a , b
的交替出現次數,列如 aaabbaaba,則 R=5。
參數設定(properties)
Hypothesis Test 目前有四種 One-sample 檢定方法,下面將個別介紹四種檢定方法的參數設定,各參數定義與預設值如下:
|
參數名稱 |
參數定義 |
預設值 |
|
View Test Results |
利用 Hypothesis Test 檢視計算結果。 |
無 |
|
TestType |
z_Test、t_Test、var_Test、runs_Test。 |
z_Test |
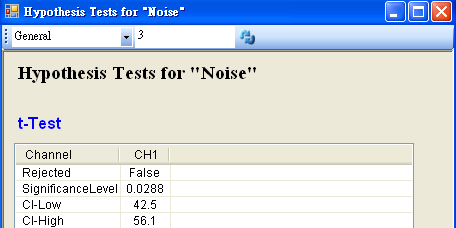
如果按下 View Test Result 將會出現檢定結果,顯示結果如下表。
|
參數名稱 |
參數定義 |
|
Rejected |
顯示檢定結果落入拒絕範圍,若顯示 True,表示可以反對虛無假設,反之則只能接受假設。 |
|
SignificanceLevel |
顯示輸入資料平均值落在母體分佈何處。 |
|
CI-Low |
虛無假設的範圍的最小值,也是信賴區間的最小值。 |
|
CI-High |
虛無假設的範圍的最大值,也是信賴區間的最大值。 |
|
Run Count |
參考理論(Theory),此值顯示即為 Runs-Test 的 R。 |
|
Above Threshold |
資料中大於設定門檻的數量。 |
|
Below Threshold |
資料中小於設定門檻的數量。 |
|
z-Value |
此結果只出現在 Runs-Test 中,表示計算出的 Z 值。 |
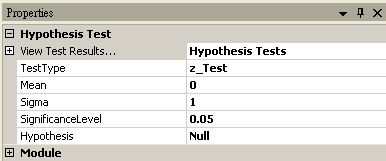
Z-Test
|
參數名稱 |
參數定義 |
預設值 |
|
Mean |
設定母體的平均值。 |
0 |
|
Sigma |
設定母體的標準差。 |
1 |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例。一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為 Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
T-Test

|
參數名稱 |
參數定義 |
預設值 |
|
Mean |
設定母體的平均值。 |
0 |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例,一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為 Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
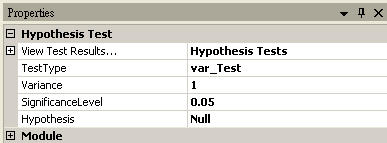
Var-Test
|
參數名稱 |
參數定義 |
預設值 |
|
Variance |
設定母體的變異數。 |
0 |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例,一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為 Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
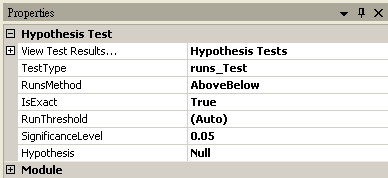
Runs-Test
|
參數名稱 |
參數定義 |
預設值 |
|
RunsMethod |
AboveBelow,UpDown。 |
AboveBelow |
|
IsExact |
計算 P-Value 是否用正確的演算法,此參數只存在 RunsMethod = AboveBelow。 |
True |
|
RunThreshold |
設定門檻,決定資料是否大於小於門檻,如果為(Auto),則是輸入資料的平均值。 |
(Auto) |
|
SignificanceLevel |
設定拒絕虛無假設的範圍,佔常態分佈面積的比例,一般常見設定為 0.1、0.05 或 0.01,設定越小,要拒絕虛無假設就越嚴苛。 |
0.05 |
|
Hypothesis |
設定檢定方法為Null (雙尾),RightTail (右尾,其中輸入資料平均值必須大於樣本平均值),LeftTail (左尾,其中輸入資料平均值必須小於樣本平均值) |
Null |
範例(Example)
本範例將舉出幾個範例,解釋各種檢定方法的使用。
-
假設一個秤重儀器,儀器釋格指出無載重時,平均重量為 0.0,標準差為 0.03,每次做實驗之前,需要經校正,利用無秤重時,讀取其顯示重量值,假設讀取 1001 次資料,利用這些資料判斷其儀器是否有偏差,首先虛無假設為儀器無偏差,進行 z-test 檢定。
-
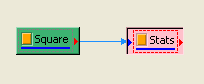
首先以 Source / Square 產生一組量測磅秤的資料,Amplitude 設定為 0.1,再連接至 Compute / Statistics / BasicStatistics,在 Basic Statistics 按下 View Statistics,觀察 Mean。
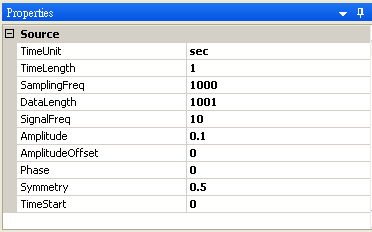
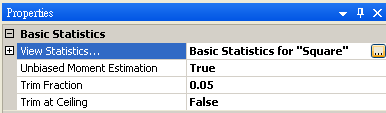

-
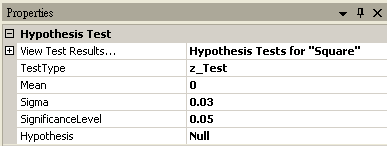
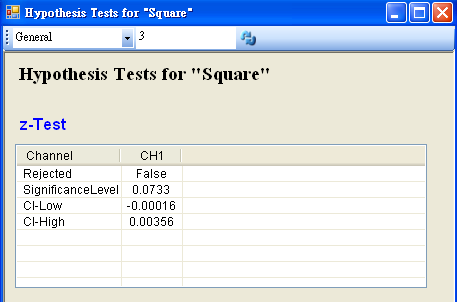
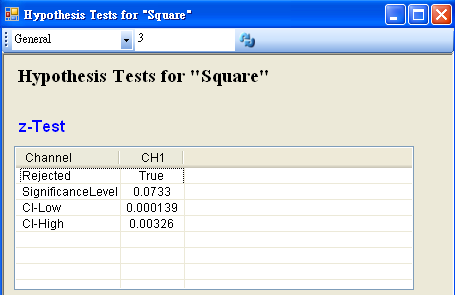
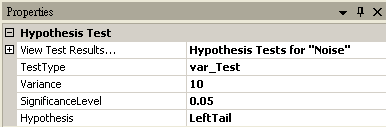
將 Square 接至 Hypothesis Test,設定 TestType = z_Test,Sigma = 0.03,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 大於預設值,虛無假設無法被拒絕,所以只能相信虛無假設,儀器並無偏差產生。
-
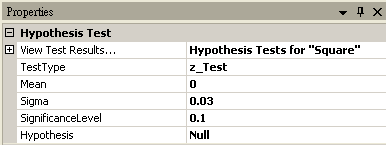
若再設定 Hypothesis Test 中 SignificanceLevel 為 0.1,將拒絕虛無假設的範圍加大,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 小於設定值,虛無假設被拒絕,所以否定虛無假設,故儀器有偏差產生,需重新加以校正。
-
假設一個班級有 51 人,因為班上導師請假,想了解班上總成績是否因故下滑,而全校成績平均 55 分,假設虛無假設為班上成績並無因為老師請假而下滑,進行 t-Test。
-
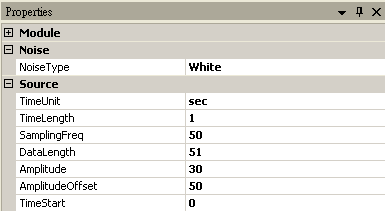
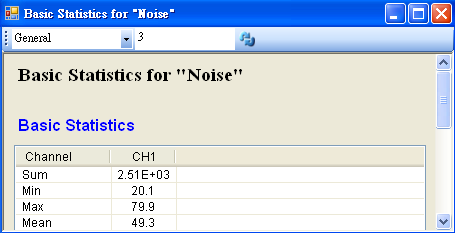
首先以 Source / Noise 產生一組學生的成績,SamplingFreq 設定為 50,Amplitude 為 30,AmplitudeOffset 為 50,再連接至 Compute / Statistics / Basic Statistics,在Basic Statistics 按下 View Statistics,觀察 Mean。
-
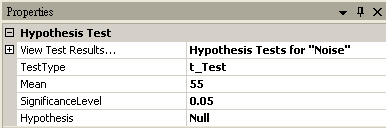
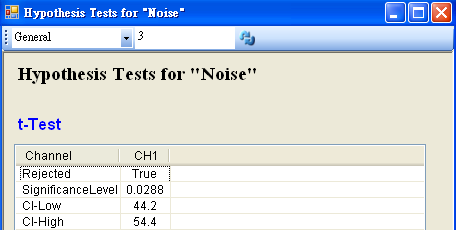
將 Noise 接至 HypothesisTest,設定 TestType = t_Test,Mean = 55,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 小於預設值,虛無假設被拒絕,所以因為老師請假而導致班上成績下滑。
-
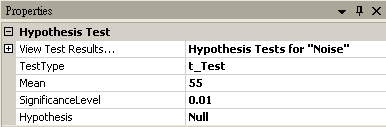
若再設定 Hypothesis Test 中 SignificanceLevle 為 0.01,將拒絕虛無假設的範圍變小,然後再以 View Test Results,觀察其檢定的結果,資料計算出的SignificanceLevel 大於設定值,虛無假設無法被拒絕,所以相信虛無假設,並不因為老師請假而造成成績下滑。
-
假設某銀行有五個窗口進行處理,客戶等待時間變異數為 10 分鐘,如今改成單一窗口處理,針對 101 位客戶進行調查,檢驗是否因為改成單一窗口之後,因此等待時間變異數變小,虛無假設為並無因為改變成單一窗口而使等待時間變異數變小,進行 Var-Test。
-
首先以 Source / Noise 產生 101 位客戶等待的時間資料,SamplingFreq 設定為 100,Amplitude 為 4.5,AmplitudeOffset 為10,再連接至 Compute / Statistics / Basic Statistics,在 BasicStatistics 按下 View Statistics,觀察 Variance。
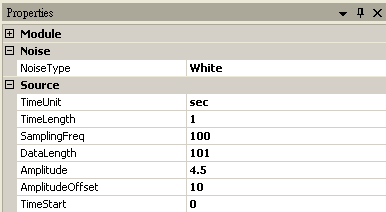
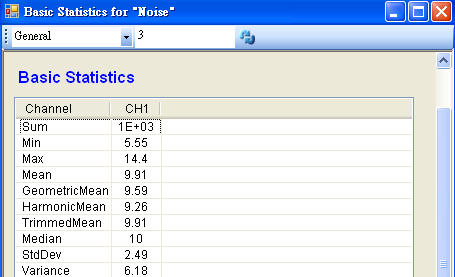
-
將 Noise 接至 HypothesisTest,設定 TestType = var_Test,Variance = 10,因為資料的變異數小於預設變異數,所以設定 Hypothsis = LeftTail,然後再以 View Test Results,觀察其檢定的結果,資料計算出的 SignificanceLevel 小於預設值,虛無假設被拒絕,因此推斷單一窗口等待時間的變異數變小。
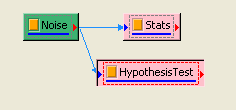

相關指令
Noise、Square、Basic Statistics
*Only in Professional *
用最小平方法算出兩組訊號的回歸線,包括線性回歸、多項式回歸、指數回歸等。此功能如同 Excel 圖表裡加上趨勢線的功能。元件上顯示的名稱為LeastSquareFit 。
最小平方法是用來計算回歸曲線的一種方法,藉由此元件計算出來的回歸曲線來近似數據與時間或是兩組數據之間的關係。本元件提供之回歸曲線種類以及其方程式如下表:
| 回歸曲線種類 | 方程式 |
|---|---|
| Linear 線性回歸 | 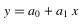
|
| Polynomial 多項式回歸 | 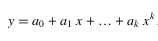
|
| PowerLaw 冪次回歸 | 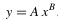
|
| Exponential 指數回歸 | 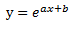
|
| Logarithm 對數回歸 | 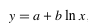
|
以線性回歸為例,我們可用方程式 y =ax+b 可說明 X 和 Y 兩組數據之間代表的物理型態。例如在驗證虎克定律的實驗裡面,通常會量測兩組數據:掛在彈簧上的砝碼重以及彈簧的總長度。接著可利用彈簧總長對砝碼重作圖,來求得彈簧的彈性係數 k,如下圖:
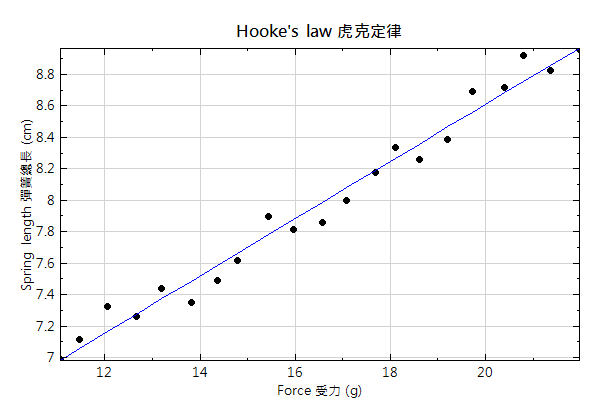
上圖黑點為量測的數據點,藍線為經由線性回歸算出來的直線。求得的線性回歸的方程式為
Spring length (彈簧總長) = 0.0907* Force(受力) + 4.99
此即彈簧總長以及受力之間的關係,同時比對虎克定律 F = kx ,上述式子可寫成
Force = 1/0.0907 * (Spring length - 4.99)
因此可知道彈簧原長為 4.99 (cm),彈簧的彈性係數為 11.02 (g/cm)。由此例子見到我們可藉由線性回歸式得到兩組數據(彈簧長度與受力)之間的關係。雖然量測數據點是離散的,但也可藉由線性回歸式來推測沒有數據之處的數值,例如從上圖可以推測受力為 20 g 時彈簧的總長約為 8.6cm 。對於在介在數據範圍內裡面不知道的xj,可以透過x * a 加上b 來得到yj;而數據範圍外的部分也可以利用線性回歸式來求得,但是由於線性方程是最簡單的近似模型,數據範圍外的預測可能會比較不準。
可是如何判定回歸線的準確度呢? 通常會利用 R square 值來說明數據點與線性方程相近的程度,也用來評估以此線性方程式來代表兩數據關係的是否可信。R sqaure 的計算可見Coefficient of Determination,是一介在0-1之間的數值,1代表完全吻合、0代表完全不吻合。因此若是要說 y=ax+b可以代表此兩組數據的話,通常會要求 R square 值在 0.95 以上(更嚴格的會要求0.99)。
使用說明
本元件把回歸分成兩種類型:
TimeSeries (線性回歸方程式為 x =at+b ),以及
XY (線性回歸方程式為 y=ax+b)
您可以在參數視窗 ( Property Window ) 看到的目前所使用的形式,注意所使用形式是*無法手動修改*的,本元件中會依照輸入數據的格式來自動判斷應該選用TimeSeries或是XY,所以務必確認您使用正確的方式連接此元件。
首先,先決定您想要知道的是 1.一組數據與時間的關係 或是 2. 兩組數據之間的關係 ,再依照下列所敘述的方法來連接。
-
一組數據與時間的關係 :形式為 TimeSeries 。
將訊號直接與本元件連接,並將用 Channel Viewer 來觀看結果。如以下流程圖:
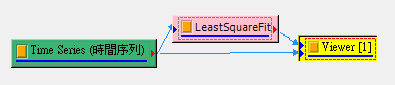
依照上述流程圖, Viewer 畫出來的圖表中有兩條線,一條為原來的時間序列,另一條為回歸後的曲線(下圖使用線性回歸),經過 Viewer 的編輯後,可以得到下列圖表。
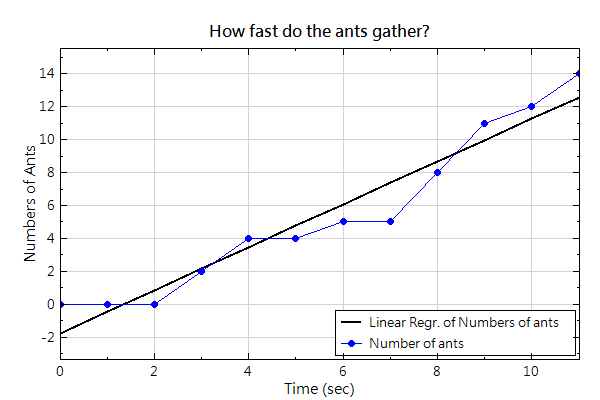
特別注意當為時間序列時,用Channel Viewer來觀看結果,不要用到 XY Plot。
-
兩組數據之間的關係:形式為 XY
將第一組數據 X 與第二組數據 Y依序連接至本元件,再將 LeastSquareFit 的結果與數據X 和 Y 連接至 Merge to Multi-Channel 合併成多通道,最後接入 XY Plot 觀看結果。連接方式如下面的流程圖:
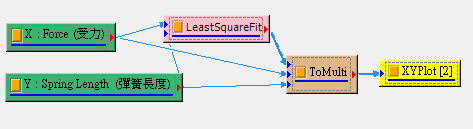
注意在連接至 ToMulti 時,連接順序必須是 LeastSquareFit, X, Y 或是 X, Y, LeastSquareFit才能在 XY Plot 圖表中正確的顯示。上述流程範例可經過 XY Plot 的編輯,產生如 說明中的虎克定律圖表:
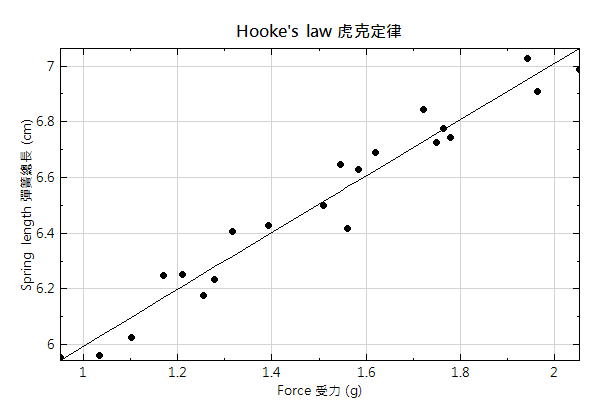
以上兩種方式為使用本元件的基本方法。
LeastSquareFit 在判斷要使用 TimesSeries 或 XY 時,是從輸入的數目來判斷。如果只有一個輸入,LeastSquareFit 會將此輸入中每一個通道的時間與數值做回歸,而輸出 x =at+b 中的 x。若有兩個輸入,則第一個輸入為X,第二組輸入為Y,使用XY方式做回歸後,輸出回歸方程式裡的 x 與 y 。若一個輸入含有多通道時,其中 TimeSeries 可以依照前段1.中流程圖把每通道中的回歸曲線以及原本數據畫出,但是使用XY線性回歸時,兩輸入的第一通道會互相配對做回歸(第二通道互相配對、第三通道互相配對...以此類推),而輸出通道依序為x1, y1, x2, y2...等等。若要將所有X-Y 配對之數據以及其回歸曲線畫出,特別注意輸入XY Plot 的通道順序必須要是x1,y1,x2,y2,...(即奇數通道與偶數通道配對),才能在圖表中正確顯示。可以參閱 XY Plot 的說明。
欲得知此回歸後的係數,找到屬性視窗中的 View Regression Parameters,會跳出如以下的方框:
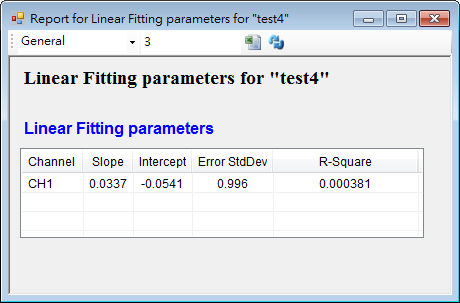
即可查詢回歸曲線的相關參數。如圖Slope 為斜率,即線性方程式中的係數 a;Intercept 為截距,即線性方程式中的b。Error StdDev 為每一數據點與回歸誤差的平均標準差,用來的得知是回歸線之可信度; R square 值也是用來得知回歸線的可信度,詳見參考資料。
參數說明
本元件接受實數(real number),單或雙通道(single or multiple channel),regular的訊號(signal)、聲音訊號(audio)輸入。相關參數說明如下表。
| 參數名稱 | 參數定義 | 預設值 |
|---|---|---|
| TimeSeries | 時間序列的回歸 | 自動選擇,無法更動 |
| XY |
兩物理量的回歸 |
自動選擇,無法更動 |
回歸曲線報表之參數定義
| 參數名稱 | 參數意義 |
|---|---|
| Channel | 通道名 |
| Error StdDev | 數據點與回歸誤差的平均標準差 |
| R-Square | Coefficient of Determination |
| Linear Fitting 線性回歸 | |
| Slope | 斜率,見公式中的 a1 |
| Intercept | 截距,見公式中的 a0 |
| Polynomial Fitting 多項式回歸 | |
| a0~an | 公式中不同項的係數 |
| PowerLaw Fitting 冪次回歸 | |
| Scale | 為公式中的A |
| Exponent | 為公式中的B |
| Exponential Fitting 指數回歸 | |
| Intercept | 為公式中的 a |
| Rate | 為公式中的 b |
| Logarithmic 對數回歸 | |
| Constant | 為公式中的 a |
| Scale | 為公式中的 b |
相關指令
XYPlot
參考資料
1. Coefficient of Determination : http://en.wikipedia.org/wiki/Coefficient_of_determination