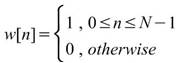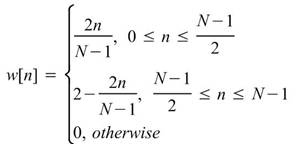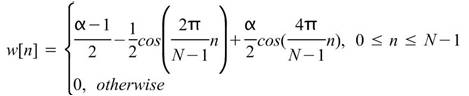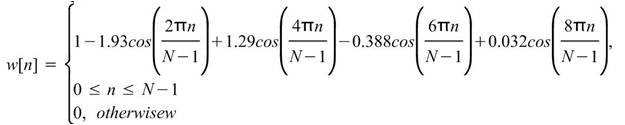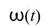本模組為提供各種訊號處理常用之轉換運算。
-
Fourier Transform/Inverse Fourier Transform:傅立葉轉換與反轉換。
-
Discrete Cosine Transform/Inverse Discrete Cosine Transform:離散餘弦轉換與反轉換。
-
Haar Wavelet Transform:小波轉換中的Haar轉換。
-
Hilbert Transform/Inverse Hilbert Transform:Hilbert轉換與反轉換。
-
Auto Correlation:計算訊號的自相關性。
-
Cross Correlation:計算訊號的交差相關性。
-
Multi-Scale Entropy(MSE):計算訊號之多尺度熵。
傅立葉轉換為將時間訊號轉換為頻率之訊號,藉此檢視訊號內之的頻率與振幅分佈,其結果可以用傅立葉反轉換計算回原始的時間訊號。此理論廣泛的應用於通信、聲音訊號、系統分析以及自然科學等領域。
說明
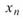 為輸入訊號的第 n
個資料,一般而言,則訊號
為輸入訊號的第 n
個資料,一般而言,則訊號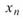 之離散傅立葉轉換為
之離散傅立葉轉換為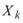 定義如下:
定義如下:
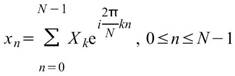
其離散傅立葉反轉換之定義如下:
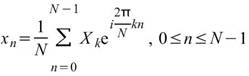
而在 Visual Signal中,離散傅立葉轉換定義為:
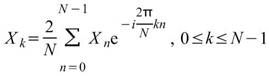
離散傅立葉反轉定義為:
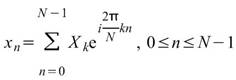
當輸入訊號,並不是周期性訊號( 既訊號頭與訊號尾並不連續且可微,此不良結果稱為洩漏效應 Spectral Leakage),插入窗函數 ( window ) 可降低 Spectral Leakage 的效應。
在離散傅立葉轉換,Resolution 屬性可用以增加頻率上的解析度。訊號長度越長,訊號的周期性越明確,所以增大 Resolution 可以增加訊號長度,可以增加頻率上的解析度。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出格式為複數,單通道,regular的訊號(signal)。參數定義與相關設定如下。
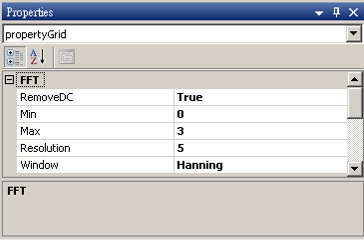
參數 RemoveDC 計算出訊號的平均值並減去,參數 Min 與 Max 可調整作傅立葉轉換的頻率範圍,Window 參數內有六種常用的窗函數,目的是將離散訊號變的較為平滑並改善因 Spectral Leakage 而造成的數值誤差。
|
參數名稱 |
參數定義 |
預設值 |
|
RemoveDC |
為消除訊號於縱軸之平移量,使訊號之平均為零。 |
True |
|
Min |
設定傅立葉轉換的頻率下限。 |
0 |
|
Max |
設定傅立葉轉換的頻率上限,大小依輸入訊號不同而異。 |
auto |
|
Resolution |
調整傅立葉轉換時採用之解析度,意思為將整個資料列重複接續在原資料後面。如原資料數列為1-100,若將resolution設為2,既為第101個數列值同第一個,第102個數列值同第二個…以此類推,持續至200。 |
1 |
|
Window |
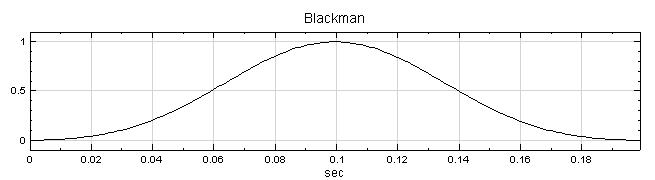
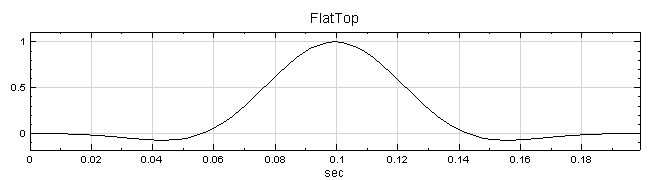
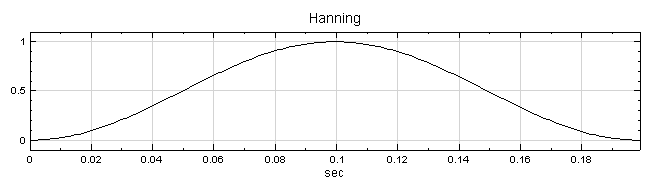
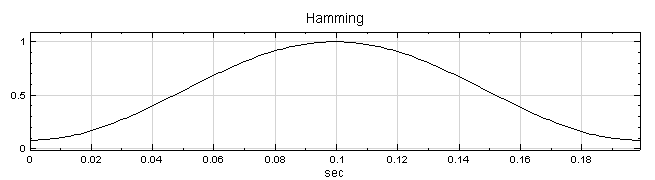
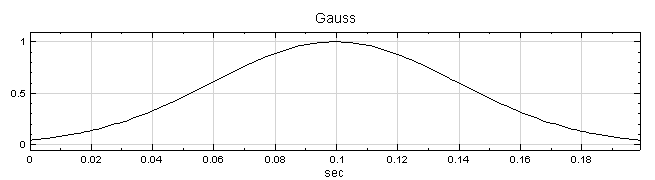
以窗函數降低洩漏效應對轉換的影響,採用之函數包括Barlett、Blackman、Flat Top、Hanning、Hamming、Gauss 等六種類型,各函數之定義詳見下節窗函數說明。 |
none |
窗函數說明(Window Function)
|
窗函數 |
定義與圖形 |
|
None |
|
|
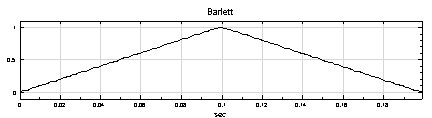
Barlett |
|
|
Blackman |
|
|
FlatTop |
|
|
Hanning |
|
|
Hamming |
|
|
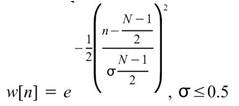
Gauss |
|
下圖為傅立葉反轉換的參數設定。
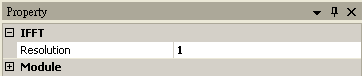
傅立葉反轉換的參數為 Resolution,意義與上述傅立葉轉換中的參數雷同,調整後,傅立葉反轉換之訊號數量將依 Resolution 值倍增。
範例(Example)
本範例(Example)運用 Source 模組產生頻率 10,TimeLength 為 0.9sec 的 sinewave,與頻率 3;TimeLength 為 0.9 的 sine wave 相加的訊號,先以 Fourier Transform 計算出訊號之頻譜,調整 Resolution 與 Window 提高頻譜的辨視度,再將頻譜以 IFFT 反轉換計算出原來的訊號。
-
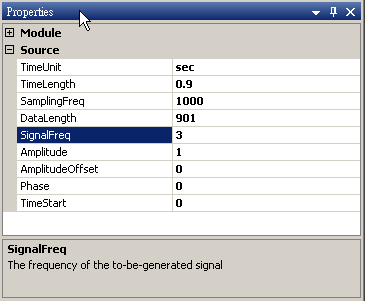
於 Network 視窗新增 Source / Sine 創造 sine wave,於 Properties 視窗 Name 欄位修改名稱為 Sine,freq=10,Signal frequency 預設即為 10 Hz,調整 TimeLength 欄位為 0.9sec。
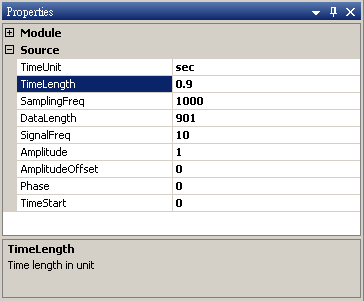
-
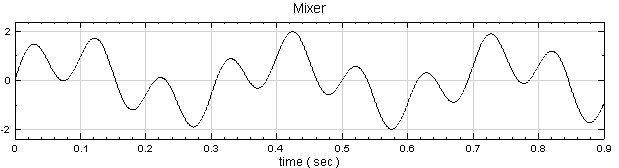
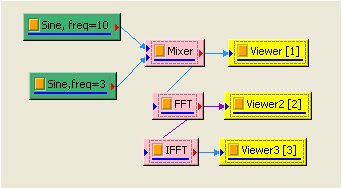
再新增一 sine wave,並設定 Signal fnequency 為 3,TimeLength 為 0.9sec 的 sine wave,再新增 Compute / Math / Mixer 模組將兩訊號相加,並用 View / Channel Viewer繪出。
-
於 Mixer 圖示上選取 Compute / Transform / Fourier Transform,即可將該訊號作傅立葉轉換,用 Channel Viewer 將頻譜繪至左邊視窗。
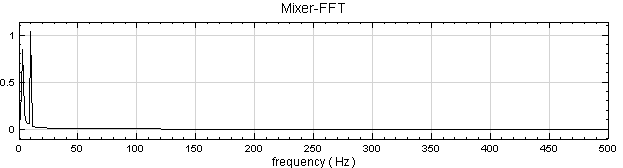
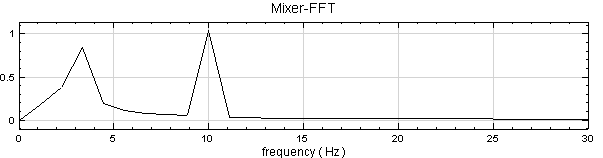 由於頻率集中在 20 以下,而
Viewer 的 Properties 內的 Xmax 預設是500,因此將該欄位設為 30,以便於觀察頻譜。
由於頻率集中在 20 以下,而
Viewer 的 Properties 內的 Xmax 預設是500,因此將該欄位設為 30,以便於觀察頻譜。
-
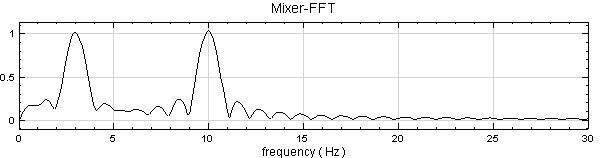
經傅立葉轉換產生的頻譜圖,可辨視主要之頻率在 10Hz 與 3Hz 處,不過 3Hz 附近的 Magnitude 被低估,可能與訊號頻率過低有關,現在調整 Resolution 來改善頻譜。於 Project 1 點選 FFT 圖示,設定 Properties / Resolution 等於 5,結果如下:
改變 Resolution 後, 3Hz 處之頻譜有明顯的改善,然而須留意改變 Resolution 後,FFT 輸出的資料長度也會隨之倍增,譬如本例輸入訊號長度為 901,經 FFT,預設 Resolution = 1 的時候,輸出長度為 451,Resolution = 5 時輸出長度則倍增五倍為 2255。
-
將 FFT 之 Resolution 調回 1,並在 FFT 圖示上點右鍵選擇 Compute / Transform / Inverse Fourier Transform,再用 Channel Viewer 輸出,即可得到原輸入訊號。
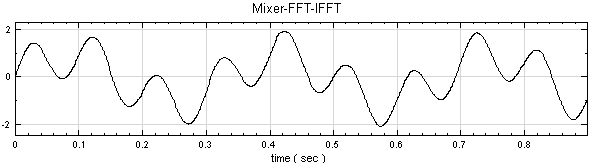
相關指令
Short-Term Fourier Transform,Haar Wavlet Transform。
參考
Discrete Cosine Transform ( 以下簡稱 DCT )離散餘弦轉換,可將訊號轉換為由 cosine 構成的序列,類似於作離散傅立葉轉換的實數部份;訊號轉換後大部份能量分佈於低頻處。其應用在音訊或影像方面的壓縮,以及求解偏微分方程的數值方法。
說明
常見的離散餘弦轉換可概分八種不同類型,本模組採用的是第二型。令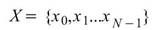 代表長度為 N
之時間序列,則離散餘弦轉換定義如下:.
代表長度為 N
之時間序列,則離散餘弦轉換定義如下:.
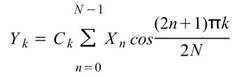 ,
,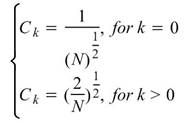
其反轉換定義如下:
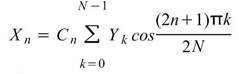 ,
,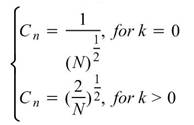
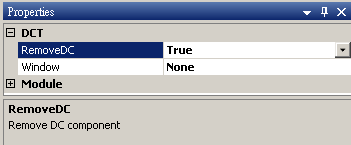
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出格式為實數,單通道,regular的訊號(signal)。離散餘弦轉換其參數設定如下,反轉換則無設定參數。
|
參數名稱 |
參數定義 |
預設值 |
|
RemoveDC |
消除訊號於振幅方向的平移量 |
Trde |
|
Window |
訊號於轉換前是否需加窗函數濾波,詳細說明可參閱FFT內容。 |
None |
範例(Example)
本範例(Example)運用 Source 產生頻率 10、TimeLength 為 0.9 sec 的 sine wave 與頻率為 3Hz,TimeLength 為 0.9sec 的 sine wave 相加的訊號。先以 DCT 計算出訊號之頻譜,再將頻譜以 Inverse DCT 計算出原來的訊號。
-
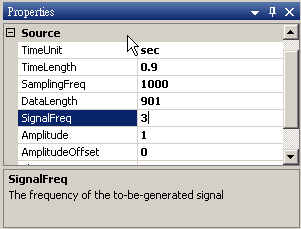
於 Network 視窗新增 Source / Sine 創造 sine wave,於 Properties 視窗調整 TimeLength 欄位為 0.9 sec。
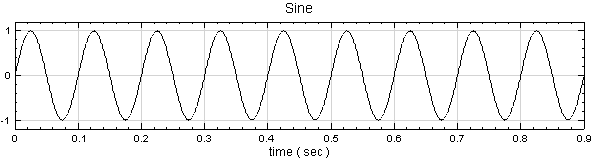
-
如上面步驟新增一 Signal frequency 為 3,TimeLength 為 0.9 sec 的 sine wave,再新增 Compute / Math / Mixer 將兩訊號相加,並用 Viewer / ChannelViewer 繪出。
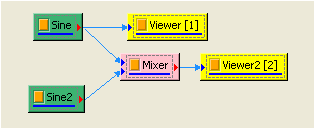
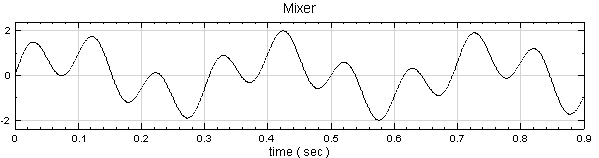
-
對 Mixer 後的訊號作 Compute / Transform / Discrete Cosine Transform,並將結果用 Channel Viewer 繪出。圖上訊號頻譜集中在低頻處。
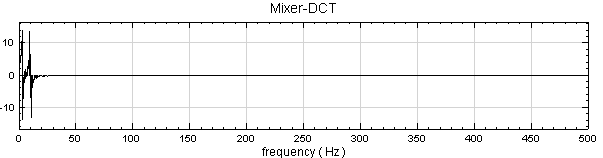
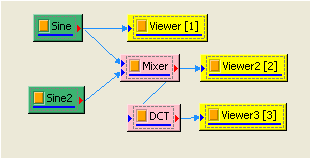
-
接著作 Compute / Transform / Inverse Cosine Transform,即轉換回原訊號。
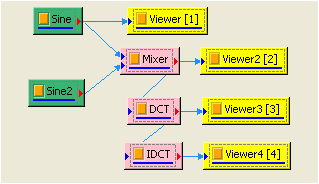
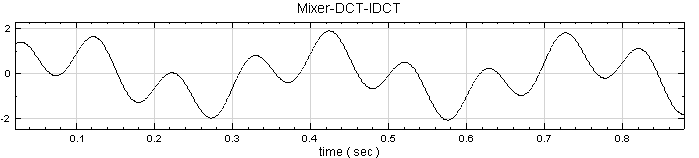
相關指令
Fourier Transform,Channel Viewer。
參考
Haar Wavelet 是首先發表的小波函式,由 Alfréd Haar 所提出,小波理論也自此發展。Haar Wavelet 是最簡單的小波,但由於不是連續函數,所以作為基本小波,性能並不是特別好。但 Haar 小波是最簡單的正交小波,為二進小波變換的基礎,仍有其存在的價值。
說明
Haar Wavelet 小波理論的母小波可由以下函式表示:
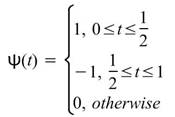
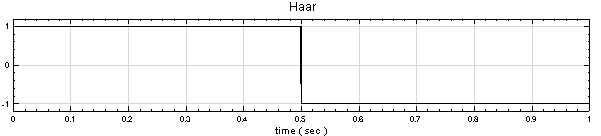
而 Haar 的傅立葉變換為:
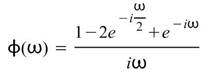
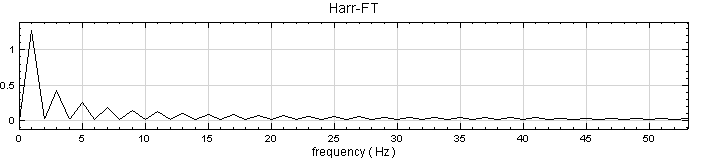
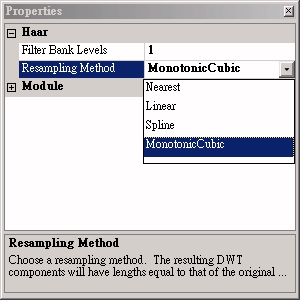
參數設定(Properties)
本模組接受實數(real number),單通道(single channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出格式為實數,多通道,regular的訊號(signal)。參數說明詳見下表。
|
參數名稱 |
參數定義 |
預設值 |
|
Filter Bank Level |
正交基底數,從零開始。1是兩組基底,5是六組基底,以此類推。 |
1 |
|
Resampling Method |
逼近方法,請參考 Resampling |
Linear |
範例(Example)
-
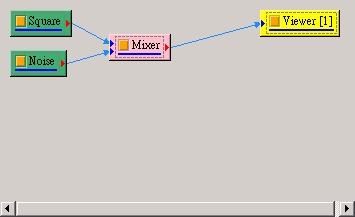
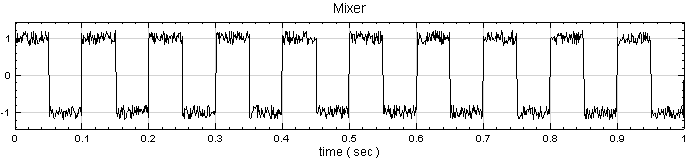
製造一個方波全採用預設值,再疊加上一 white noise 並設noise 振幅為 0.2。
-
將此混合後之訊號接上 Compute / Transform /Haar transform,並設定 Filter Bank level 為 3 :
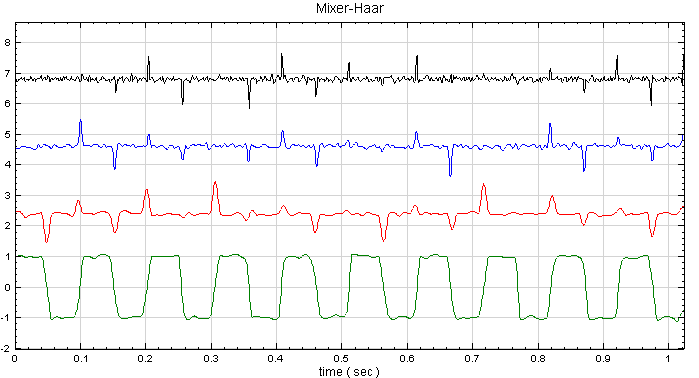
明顯方波的特性集中在第四條,而在原方波不連續點處,第二與三條依然強烈地保留此跳躍特性,高頻雜訊大多集中在第一條。
-
將第二與第三訊號相乘,以縮小雜訊所造成的影響,再與第四條相加。
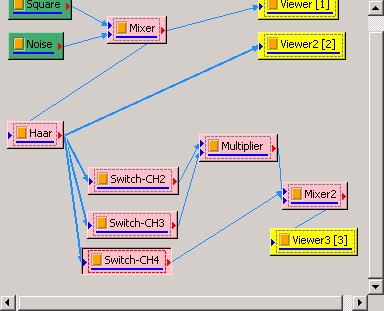
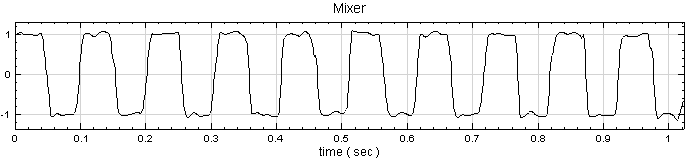
如此處理,可見雜訊被消除,原方波的特性被保留下來。
-
類似於 EMD,可將 HaarTransform 後的結果經由 Hilbert Spectrum 處理,即可看到時頻圖:
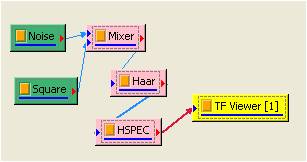
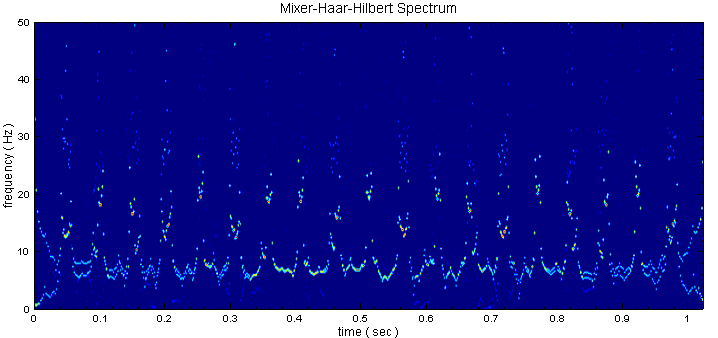
相關指令
Mixer,Multiplier,Fourier Transform,Hilbert Spectrum
參考
http://amath.colorado.edu/courses/4720/2000Spr/Labs/Haar/haar.html
Hilbert transform 為對輸入訊號 與
與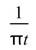 作折積(即
Convolution
),將一個實數的時間訊號轉換為一個複數平面上的解析訊號,而它的實部為輸入訊號,虛部則是對輸入訊號做折積後的部份,
根據解析訊號的性質可定義出訊號瞬時的瞬時頻率、瞬時振幅,其應用在通訊系統及無線電訊號處理及分析上有相當不錯的成果。
作折積(即
Convolution
),將一個實數的時間訊號轉換為一個複數平面上的解析訊號,而它的實部為輸入訊號,虛部則是對輸入訊號做折積後的部份,
根據解析訊號的性質可定義出訊號瞬時的瞬時頻率、瞬時振幅,其應用在通訊系統及無線電訊號處理及分析上有相當不錯的成果。
說明
若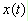 代表時間序列,則它的 Hilbert
Transform
代表時間序列,則它的 Hilbert
Transform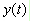 定義為:
定義為:
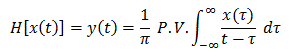
並定義一解析函數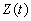 :
:
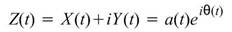 ,
,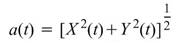 ,
,
其中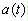 為振幅(亦原訊號之包絡線),而
為振幅(亦原訊號之包絡線),而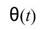 為相角;在解析函數
為相角;在解析函數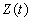 的極座標表示中,可進一步定義 Hilbert Transform
的瞬時頻率
的極座標表示中,可進一步定義 Hilbert Transform
的瞬時頻率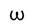 (instantaneous frequency):
(instantaneous frequency):
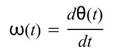
模組之輸出
除此之介紹外,可參考 Hilbert Spectrum。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出格式為複數,單通道,regular的訊號(signal)。
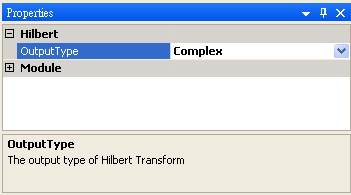
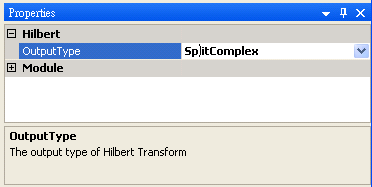
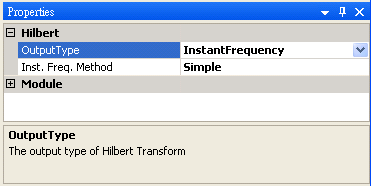
Hilbert transform 的參數為 Output Type,設定轉換結果呈現的格式,選項有 Complex、Split Complex、Phase、InstantFrequency 與 Instant Amplitude 等,其中 InstantFrequency 演算上可分為 Simple 法 與 Barne 法,各選項之意義詳見下表說明。
|
選項名稱 |
意義 |
|
Complex |
輸出解析訊號Z,資料儲存為複數。 |
|
SplitComplex |
將解析訊號 Z 的實部 X 與虛部 Y 分作兩個通道,儲存其數值大小。 |
|
Phase |
解析訊號 Z 的相位角 |
| Unwrapped Phase | 解析訊號 Z 的相位角 對應各時間點的值(過360度後不歸零)。 對應各時間點的值(過360度後不歸零)。 |
|
InstantAmplitude |
解析訊號 Z 的振幅 |
|
InstantFrequency |
解析訊號 Z 的相位角 |
範例 ( Example )
範例 I :用 Source 模組產生一個 sine wave 訊號,直接作 Hilbert Transform,並藉調整 Hilbert transform 的 Output Type 以瞭解各參數項之意義。
-
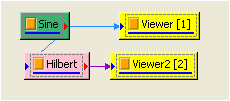
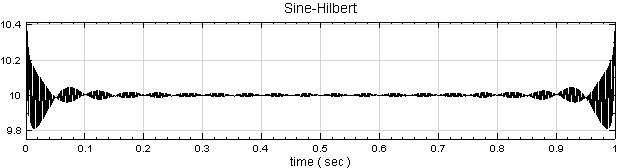
先用 Source / Sine Wave 產生 sine wave,用 Viewer / ChannelViewer 繪出訊號,再於 Sine 圖示點選 Compute / Transform / Hilbert Transform 直接作計算,Output Type 預設為 Complex,用 Viewer / Channel Viewer 繪出結果。(須注意輸出訊號是複數,而 Channel Viewer 的 Properties / YValueType 預設是 Magnitude,因此在 Viewer 上畫的是輸出訊號的 Magnitude )。
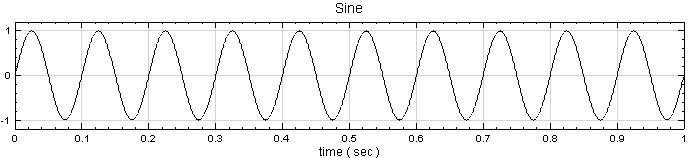
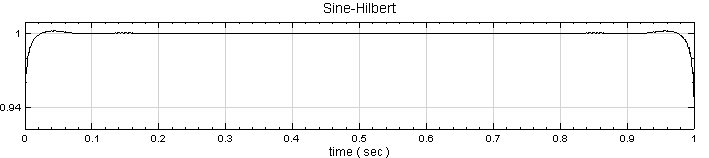
若將 Sine 與Hilbert Spectrum 輸出者畫在同一個 Channel Viewer上,可見
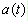 確實為原訊號之包絡線。
確實為原訊號之包絡線。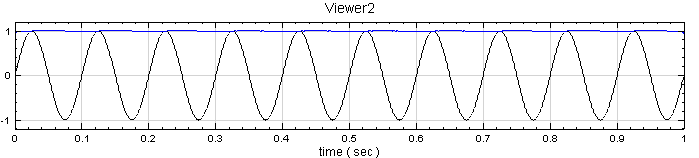 )
) -
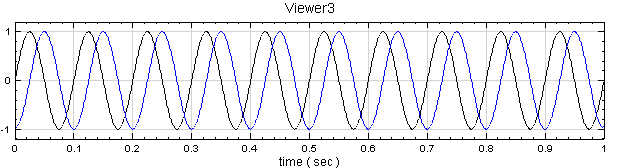
對訊號源 Sine 再作一次 Hilbert Transform,將 Properties 內 Hilbert / Output Type調整為 Split Complex,這樣 Hilbert Transform 會把實、虛部分為兩個通道,用 Viewer / Channel Viewer 即繪出實部與虛部的值,其中黑線為實部,藍線為虛部。
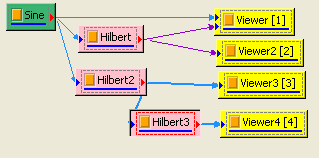
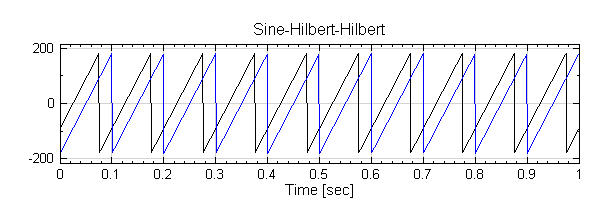
再將Hibert2再作一次 Hilbert Transform,將 Properties 內 Hilbert / Output Type調整為phase, 可看到虛部為實部對相位角作 90∘的相位偏移 ( phase shift ) 。
-
重覆步驟 2 的作法,僅改變 Output Type 為 InstantFrequency,圖示名稱也改為 Instant Frequency,結果為輸入訊號在每個時間點上的瞬間頻率。
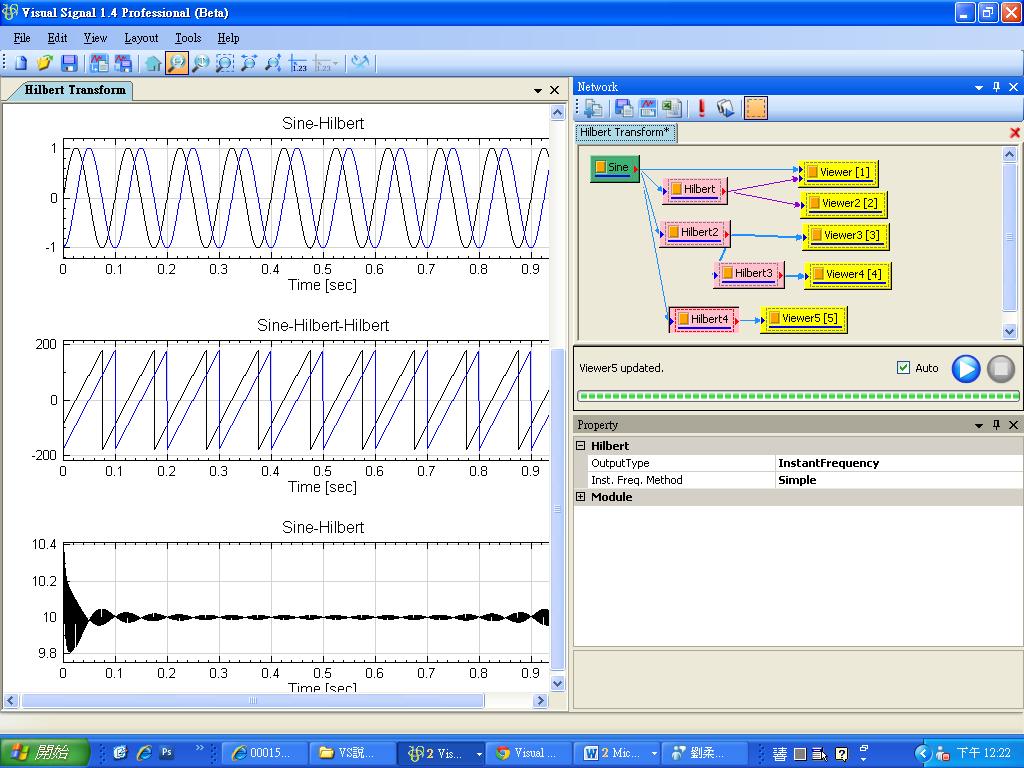
-
Channel Viewer 不能繪出解析函數 Z(t) 在複數平面的圖型,必需使用 Viewer / XYPlot 的功能。將 Split Complex 的輸出用 Viewer / XYPlot 即可繪出解析函數 Z(t) 在複數平面的圖型,改變 XYPlot 的 ViewerWidth 與 ViewerHeight 為相等的數值(如 350 ),就能使 XY 軸的比例一樣。
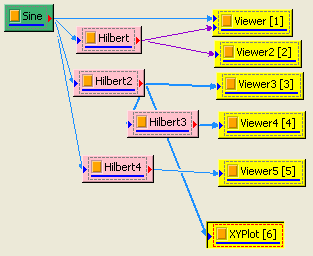
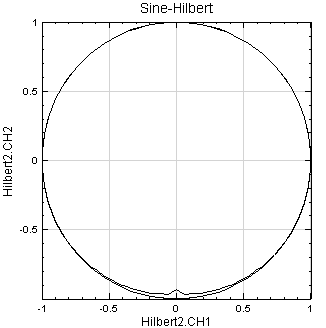
相關指令
參考資料
自我相關性就是一個時間訊號與它自身作折積 ( Convolution ),以作為相關性分析之依據,自我相關性分析可瞭解一個訊號在時間尺度上改變的有多快,及觀察訊號是否有週期性的變化。
說明
自相關的的解析定義為:
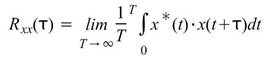 ,其中
,其中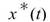 為
為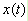 之共軛,
之共軛,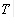 為訊號之週期,
為訊號之週期,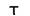 為時間延遲。
為時間延遲。
在離散化的情況下,令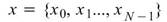 代表長度為N之時間序列,相關公式為:
代表長度為N之時間序列,相關公式為:
 ,
,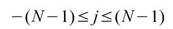
而在![]() 時
時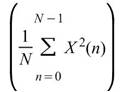 ,等同均方值
,等同均方值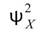
參數設定(Properties)
本模組接受實數(real number),單通道(single channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出訊號格式為實數,單通道,regular的訊號。本模組無其它的參數設定。
範例(Example)
本範例分別對 sine wave 與一個 white noise 訊號作自我相關分析,再以兩輸入訊號混合後之訊號作自我相關分析。
-
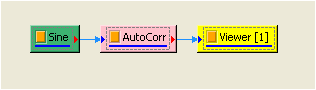
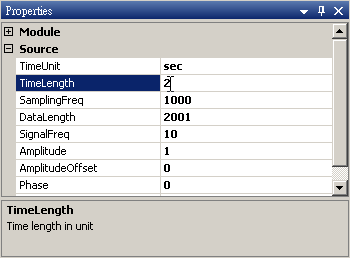
於 Network 新增一個 Source / Sine Wave,Properties /DataLength 改為 2 sec,訊號頻率為 10Hz 不變,以此訊號作 Compute / transform / AutoCorrelation ,並用 Viewer / Channel Viewer 繪出結果。
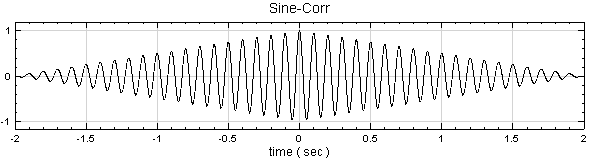
-
上圖即為 sine wave 在不同延遲(既原式中的
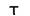 )下之自我的相關性,對 AutoCorr 的輸出作
FFT,可發現 AutoCorr 的輸出訊號其頻率也等於
10,驗證對一個週期性訊號作自我相關轉換,則結果保有與輸入訊號同樣的頻率。
)下之自我的相關性,對 AutoCorr 的輸出作
FFT,可發現 AutoCorr 的輸出訊號其頻率也等於
10,驗證對一個週期性訊號作自我相關轉換,則結果保有與輸入訊號同樣的頻率。

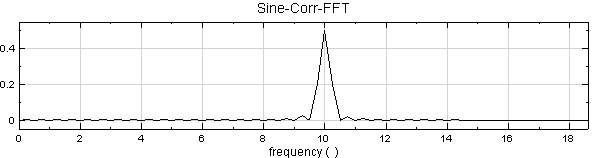
-
創造一個 White noise,再重複步驟1前半部份的作法,結果如下。
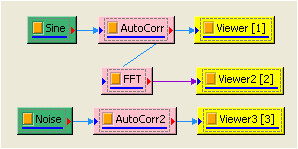
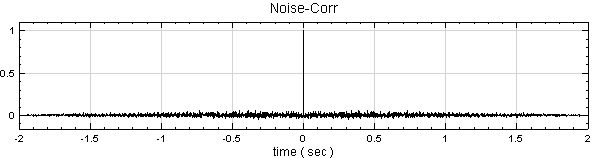
-
以 Compute / Channel / Mixer 將 Sine 與 Noise 混合後作自我相關分析,可得到下面的結果:
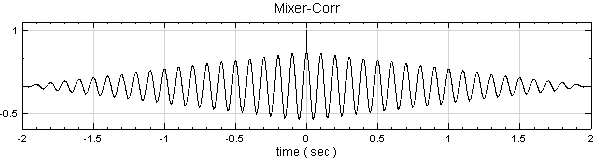
相關指令
Cross Correlation,Mixer。
參考
CrossCorrelation,交互關聯是將一時間訊號與另一時間訊號作旋積 ( Convolution ),以作為相關性分析之依據;通常將不了解的訊號與一已知性質的訊號作交叉相關分析,藉此探求該訊號之特性。
說明
CrossCorrelation 之解析數學定義為:
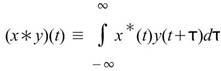 ,
,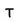 為時間延遲項。
為時間延遲項。
在離散數列的情況下,假設 、
、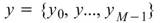 在延遲為
在延遲為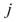 的交互關聯定義為:
的交互關聯定義為:
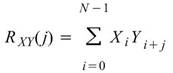 ,
,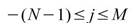
交叉相關轉換結果訊號長度為 N+M-1,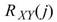 不具對稱性,其最大值遵守下述的不等式:
不具對稱性,其最大值遵守下述的不等式:
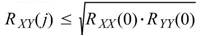
若對兩輸入訊號在統計上來說是兩獨立事件,則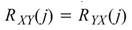 ;若是分析訊號對自身的相關性,計算
;若是分析訊號對自身的相關性,計算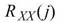 ,此分析即為Auto Correlation。
,此分析即為Auto Correlation。
參數設定(Properties)
本模組接受實數(real number),單通道(single channel),regular的訊號(signal)、聲音訊號(audio)輸入,且須有兩個輸入訊號;輸出訊號格式為實數,單通道,regular的訊號。輸入兩個訊號長(可以不一樣,不過限制是兩訊號的取樣頻率與時間單位必須一樣。
範例(Example)
先產生一組white noise 作原訊號,截取其中一段資料,產生另一個雜訊合成出第二組訊號,以這兩組訊號作 Cross Correlation 觀察兩者間關係。
-
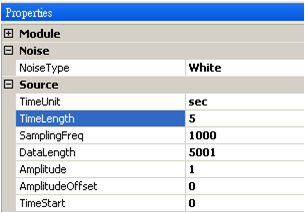
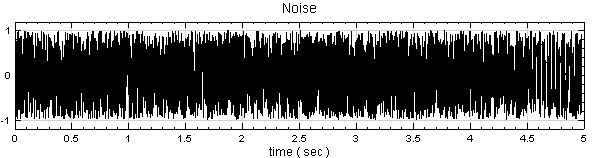
產生一個 Source / Noise,Properties / TimeLength改為 5 sec,再用 Viewer / Channel Viewer 繪出。
-
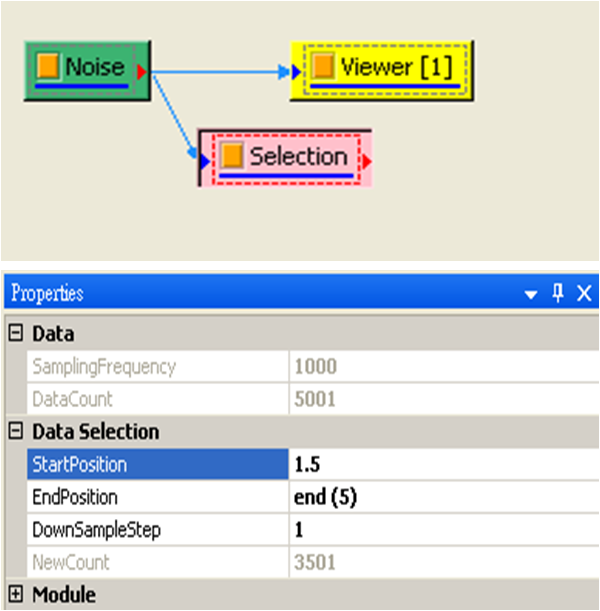
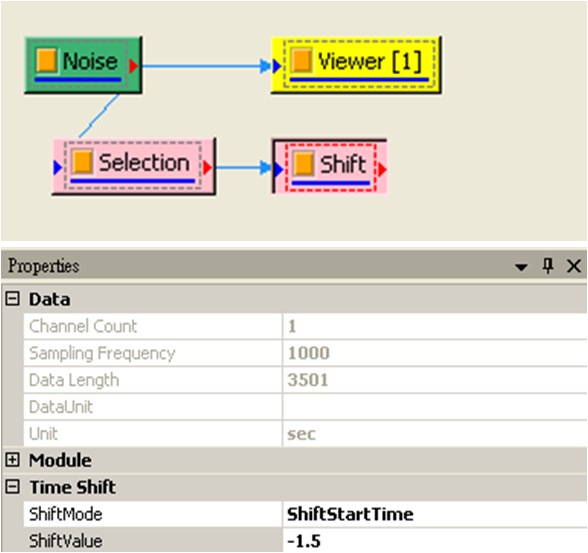
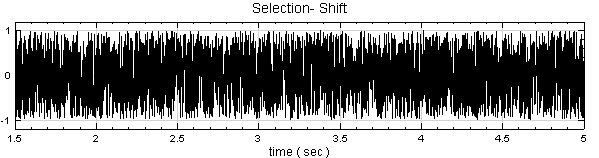
點選 Noise,按右鍵選擇 Compute / Channel / Data Selection,於 Properties / EndPosition欄改為 3.5,然後接著連上 Compute / Channel / Time Shift,Properties / Shift Value 設為 -1.5,目的為將原訊號 0 ~ 3.5 秒的資料移至新訊號 1.5 ~ 5 秒處。
-
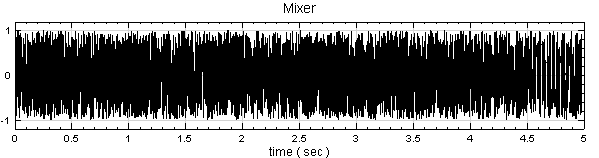
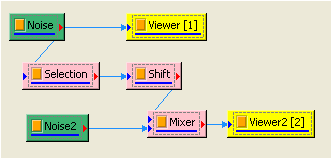
再產生一組 TimeLength 為 1.5 sec的 Noise,將此 noise 與 Time Shift 後的訊號作 Compute / Channel / Mixer 形成第二個訊號源,再以 Channel Viewer 繪出。
-
將訊號 Noise 與 Mixer 一起作 Cross Correlation,再用 Channel Viewer 繪出結果。
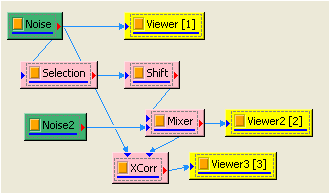
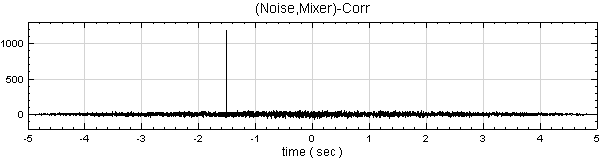
上圖代表輸入訊號 1 與訊號2 在時間點為 -1.5 sec 時有很強的相關性,基本上第二個輸入訊號在 1.5 sec 至 5 sec 的資料與第一個輸入訊號 0 sec 至 3.5 sec 的資料是完全一樣的,此結果符合兩輸入訊號的特性。
相關指令
Auto Correlation,Data Selection,Mixer,Time Shift。
MSE是Multiscale Entropy(多尺度熵)之縮寫,是分析系統的時間序列的複雜度。複雜度越高代表系統愈健康。此法可應用於分析生物(biological)、地球科學(earth science)及機械振動(mechanical vibration)的訊號。
此複雜度的意義與傳統熵 (Entropy) 值有所不同;在傳統熵值觀念中若系統愈規則熵值愈低反之系統愈混亂熵值愈高。在新的観念中,複雜度愈高代表系統愈健康(在此高低是相對量),系統太規則或系統太混亂都是不健康的狀況(因為此時複雜度較健康系統低)。將每個尺度的時間序列,計算出對應的熵值,即為多尺度訊號熵分析,訊號的複雜度則展現在多種尺度下熵值的變化。
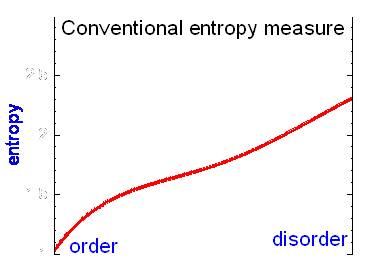
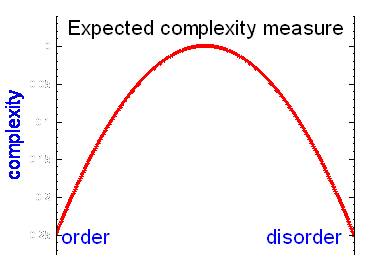
本模組中熵的計算的採用 Sample Entropy。它改進了 Approximate Entropy;更具體的說,它比 Approximate Entropy 所需的資料量更短。
多尺度的概念,假設尺度(scale)為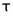 則該尺度下之時間序列
則該尺度下之時間序列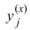 經定義表示為 :
經定義表示為 :
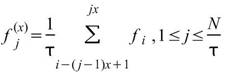
數列中每個點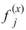 即為每尺度內之平均數。對於每個尺度
即為每尺度內之平均數。對於每個尺度 計算 Sample Entropy :
計算 Sample Entropy :
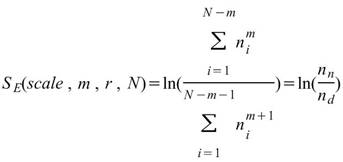
在上式中,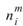 表式滿足
表式滿足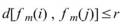 其中 d 是為歐幾里德幾何學中的距離函數 :
其中 d 是為歐幾里德幾何學中的距離函數 :
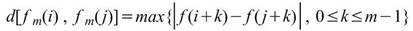
參數設定(Properties)
本模組接受實數(real number),單通道(single channel)或多通道(multi-channel),regular的訊號(signal)、聲音訊號(audio)輸入;輸出訊號格式為實數,單通道或多通道,regular的訊號。參數說明詳見下表。
|
參數名稱 |
參數定義 |
預設值 |
|
MinScale |
最小尺度。作多尺度分析時設定尺度縮放之下限值 |
1 |
|
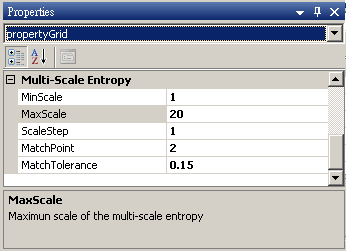
MaxScale |
最大尺度。作多尺度分析時設定尺度縮放之上限值 |
20 |
|
ScaleStep |
尺度步長,於尺度上限以下取一步幅長,依此步幅長遞增(減)尺度至最大(小)尺度。 |
預設值=1 |
|
MatchPoint |
設定比較相似度之數列長度 |
2 |
|
MatchTolerance |
判斷相似度所設定的容忍誤差值,即原式中的 r |
0.15 |
範例(Example)
本範例針對人體生理訊號為分析:
-
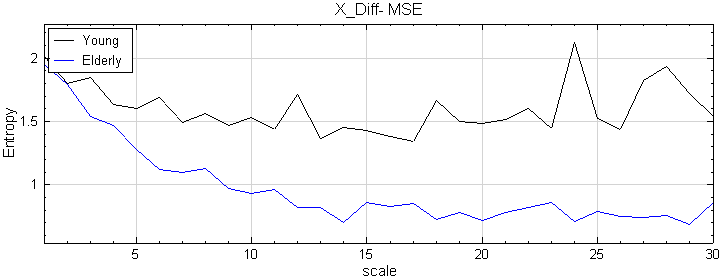
於Project 視窗下,載入兩筆資料,分別為年輕人及老年人站立時的 Center of Pressure (COP),在 X 方向隨時間的變化,利用 Viewer / Channel Viewer 觀察結果。

-
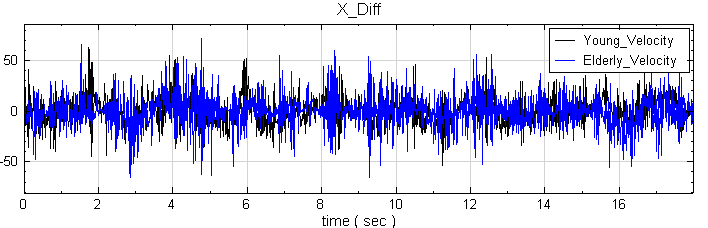
為了解保持身體平衡的能力,再將其原始訊號經過微分,得到 COP 的速度變化,如下圖。
-
最後將兩速度訊號經過 Compute / Transform / MSE 計算,利用 Viewer / Channel Viewer 觀察結果,發現年長者平衡感較差,COP 之改變較無彈性,是故熵隨尺度變大而衰減;而年輕人平衡感好,COP 移動靈活,熵幾不隨尺度而改變。
-
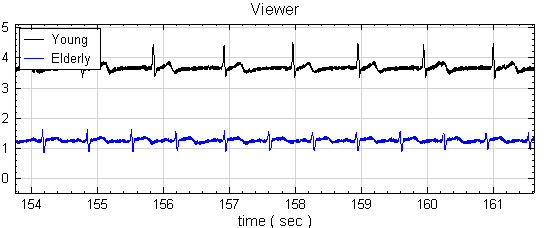
再討論另一個例子,18 歲健康年輕人及 55 歲健康中年人,分別量取其 ECG,ECG 結果如下圖顯示。
-
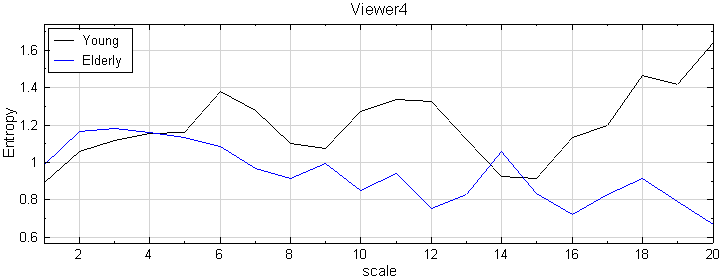
分別將兩個人的 ECG 分別計算出兩心跳間的時距,即所謂的 RRinterval ,最後利用 MSE 計算,其結果如下圖。並可以解釋年輕人的 ECG 與中年人的 ECG 作比較,年輕人的訊號複雜度較中年人來的高,年輕人心臟比較能應付外在各種變化,並進行調節心臟跳動。
相關指令
Noise,Viewer。
參考資料
1. Pincus, S. M., Approximate entropy as a measure of system complexity, Proceedings of the NationalAcademy ofSciences, USA, Vol. 88, pp. 2297-2301 (1991).
2. Costa M., Goldberger A.L., Peng C.-K. Multiscale entropy analysis of physiologic time series. Phys Rev Lett 2002; 89:062102.
3. Costa M, Peng C-K, Goldberger AL, Hausdorff JM. Multiscale entropy analysis of human gait dynaiics. Physica A ,2003;330:53-60.
4. Costa M., Goldberger A.L., Peng C.-K. Multiscale entropy analysis of biological signals. Phys Rev E 2005;71:021906.